摄像机模型 ¶
约 3055 个字 1 张图片 预计阅读时间 10 分钟
Abstract
- 摄像机是 3D 世界(物体空间)和 2D 图像之间的映射。多视图中主要关心中心投影。
- 具体模型主要分成有限中心的摄像机模型和“无穷远”中心的摄像机模型。
- 本章主要讨论点的投影。
有限摄像机 ¶
基本针孔模型 ¶
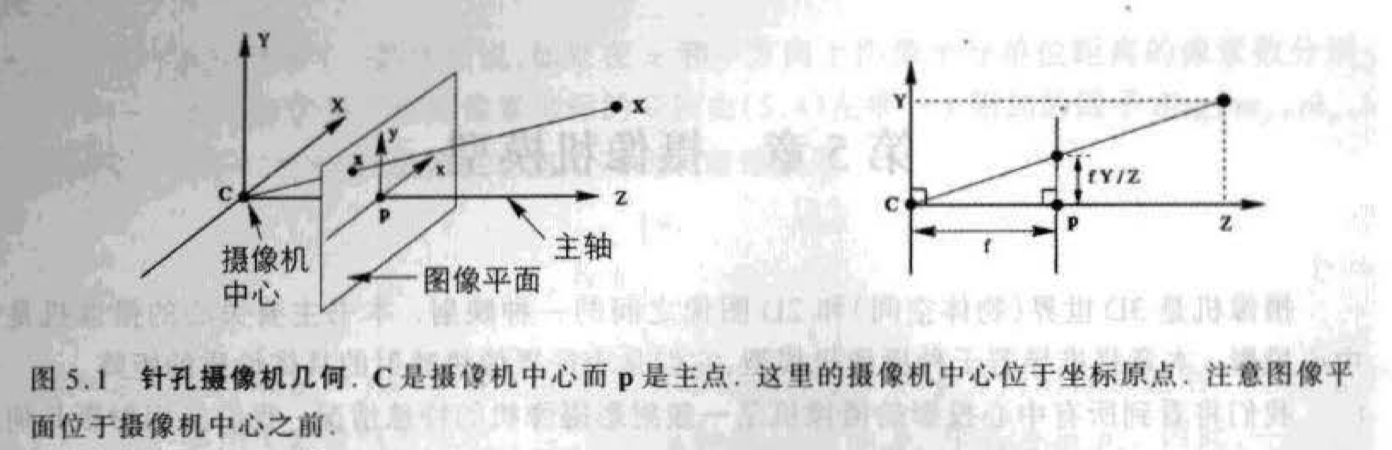
- 令投影中心位于一个欧氏坐标系的原点,而平面 \(Z=f\) 被称为图像平面或聚焦平面。
- 在针孔模型下,空间坐标为 \(\mathbf{X}=(X,Y,Z)^\top\),从世界坐标到图像坐标的中心投影为 \((X,Y,Z)^\top \to (fX/Z,fY/Z)^\top\)
- 射影中心称为摄像机中心,也成光心。
-
摄像机中心到图像平面的垂线称为摄像机的主轴或主射线,而主轴与图像平面的交点称为主点,过摄像机中心平行于图像平面的平面称为摄像机的主平面。
-
用齐次坐标表示中心投影:
\[
\begin{bmatrix}
X \\
Y \\
Z \\
1
\end{bmatrix}
\to
\begin{bmatrix}
fX \\
fY \\
Z
\end{bmatrix}
=
\begin{bmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
Z \\
1
\end{bmatrix}
\\
\\
上式也可表示为 \ \ \ \mathbf{x}=P\mathbf{X} \ \ \ 其中 \ \mathbf{X}用四维齐次矢量(X,Y,Z,1)^\top 表示 \ P = diag(f,f,1)[\mathbf{I}|\mathbf{0}]
\]
-
主点偏置
- 上面讨论的图像平面的坐标原点在主点上,但实际上可能不是,一般情形的映射为 \((X,Y,Z)^\top \to (fX/Z+p_x,fY/Z+p_y)^\top\),根据上式推导:
\[ \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} \to \begin{bmatrix} fX+Zp_x \\ fY+Zp_y \\ Z \end{bmatrix} = \begin{bmatrix} f & 0 & p_x & 0 \\ 0 & f & p_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \\ \end{bmatrix} \]- 令 \(K = \begin{bmatrix} f & 0 & p_x \\ 0 & f & p_y \\ 0 & 0 & 1 \end{bmatrix}\), 则有 \(\mathbf{x}=K[\mathbf{I}|\mathbf{0}]\mathbf{X}_{cam}\),其中点 \(\mathbf{X}_{cam}\) 是摄像机坐标系,矩阵 \(K\) 称为摄像机标定矩阵(内参矩阵),\([\mathbf{I}|\mathbf{0}]\) 称为外参矩阵。
-
摄像机旋转与位移
\[
X_{cam}=
\begin{bmatrix}
R & -R\tilde{\mathbf{C}} \\
\mathbf{0}^\top & 1
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
Z \\
1
\end{bmatrix}
=
\begin{bmatrix}
R & -R\tilde{\mathbf{C}} \\
\mathbf{0}^\top & 1
\end{bmatrix}
\mathbf{X}
\\
\mathbf{x}=KR[\mathbf{I}|-\tilde{\mathbf{C}}]\mathbf{X}
\]
- 一般的针孔摄像机 \(P=KR[\mathbf{I}|-\tilde{\mathbf{C}}]\) 有 9 个自由度;3 个来自 \(K\),3 个来自 \(R\),3 个来自 \(\tilde{\mathbf{C}}\)。\(K\) 中的参数称为摄像机内部参数或摄像机的内部校准。\(R\) 和 \(\tilde{\mathbf{C}}\) 并称为外部参数或外部校准。摄像机矩阵可简化成:
\[
\mathbf{P}=K[R|\mathbf{t}],其中 \ \mathbf{t}=-R\tilde{\mathbf{C}}
\]
CCD 摄像机 ¶
- CCD 摄像机的像素可能不是正方形,如果图像坐标以像素来测量,那么需要在每个方向上引入非等量尺度因子。
- 一般形式:
\[
K=
\begin{bmatrix}
\alpha_x & 0 & x_0 \\
0 & \alpha_y & y_0 \\
0 & 0 & 1
\end{bmatrix}
\]
- 其中 \(\alpha_x=fm_x, \alpha_y=fm_y,x_0=m_xp_x,y_0=m_yp_y\)。\(m_x,m_y\) 分别是在 x 和 y 方向上图像坐标单位矩阵的像素数。
- 一个 CCD 摄像机有 10 个自由度。
有限射影摄像机 ¶
- 考虑形如下面的标定矩阵,增加的参数 s 称为扭曲参数,对大多数标准的摄像机来说,其扭曲参数为 0。
\[
K=
\begin{bmatrix}
\alpha_x & s & x_0 \\
0 & \alpha_y & y_0 \\
0 & 0 & 1
\end{bmatrix}
\]
- 一个有限射影摄像机有 11 个自由度。
射影摄像机 ¶
摄像机构造 ¶
- 一般射影摄像机可以按 \(P=[M|\mathbf{p}_4]\) 分块,其中 \(M\) 是 \(3 \times 3\) 矩阵,如果 \(M\) 是非奇异的,那么它是有限摄像机,反之则不然
- 摄像机中心:摄像机中心 \(C\) 是 \(P\) 的一维右零空间,即 \(P \mathbf{C}=\mathbf{0}\)
- 有限摄像机(M 非奇异)\(\mathbf{C}=\begin{bmatrix} -M^{-1}\mathbf{p}_4 \\ 1 \end{bmatrix}\)
- 无穷远摄像机(M 奇异)\(\mathbf{C} = \begin{bmatrix} \mathbf{d} \\ 0 \end{bmatrix}\),其中,\(\mathbf{d}\) 是 \(M\) 的 3 维零矢量,即 \(M \mathbf{d}=\mathbf{0}\)
- 列点:对于 \(i=1,..,3\),列矢量 \(\mathbf{p}_i\) 分别对应于 \(X,Y,Z\) 轴在图像上的消影点。列 \(\mathbf{p}_4\) 是坐标原点的图像
- 主平面:摄像机的主平面是 \(P\) 的最后一行 \(\mathbf{P}^3\)
- 轴平面:平面 \(\mathbf{P}^1\) 和 \(\mathbf{P}^2\)(\(P\) 的第一和第二行)表示空间中过摄像机中心的平面,分别对应于映射到图像上直线 \(x=0\) 和 \(y=0\) 的点
- 主点:图像点 \(\mathbf{x}_0=M\mathbf{m}^3\) 是摄像机的主点,其中 \(\mathbf{m}^{3\top}\) 是 \(M\) 的第三行
- 主射线:摄像机的主射线(主轴)是过摄像机中心 \(\mathbf{C}\) 而方向矢量为 \(\mathbf{m}^{3\top}\) 的射线。主轴矢量 \(\mathbf{v}=\det(M)\mathbf{m}^3\) 指向摄像机的前方
射影摄像机对点的作用 ¶
- 正向投影:在无穷远平面上的点 \(\mathbf{D}=(\mathbf{d}^\top,\mathbf{0})^\top\) 表示消影点,这些点映射到 \(\mathbf{x}=P\mathbf{D}=[M|\mathbf{p}_4]=M\mathbf{d}\)
-
点到射影的反向投影:
- 给定图像中的一个点 \(\mathbf{x}\) 来确定是空间的那些点被映射到该点。这些点交组成过摄像机中心的一条空间射线:\(\mathbf{X}(\lambda)=P^+\mathbf{x}+\lambda\mathbf{C}\) 其中 \(P^+\) 是 \(P\) 的伪逆。\(P^+=P^\top(PP^\top)^{-1}\) 并且 \(PP^+=I\)
- 一个图像点 \(\mathbf{x}\) 反向投影的射线交无穷远平面于点 \(\mathbf{D}=((M^{-1}\mathbf{x})^\top, 0)^\top\)。将射线写成其与摄像机中心的两点的连接 :
\[ \mathbf{X}(\mu)=\mu\begin{bmatrix}M^{-1}\mathbf{x}\\0\end{bmatrix}+ \begin{bmatrix}-M^{-1}\mathbf{p}_4\\1\end{bmatrix}= \begin{bmatrix}M^{-1}(\mu\mathbf{x}-\mathbf{p}_4)\\1\end{bmatrix} \]
点的深度 ¶
- 令 \(\mathbf{X}=(X,Y,Z,T)^\top\) 是一个 3D 点而 \(P=[M|\mathbf{p}_4]\) 是一个有限摄像机的摄像机矩阵,假定 \(P(X,Y,Z,T)^\top=w(x,y,1)^\top\),那么 \(depth(\mathbf{X};P)=\frac{sign(\det M)w}{T\parallel \mathbf{m}^3 \parallel}\) 是在摄像机主平面前方的点 \(\mathbf{X}\) 的深度
摄像机矩阵的分解 ¶
- 求摄像机中心:中心 \(\mathbf{C}=(X,Y,Z,T)^\top\),其中
- \(X=\det([\mathbf{p}_2, \mathbf{p}_3, \mathbf{p}_4])\)
- \(Y=-\det([\mathbf{p}_1, \mathbf{p}_3, \mathbf{p}_4])\)
- \(Z=\det([\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_4])\)
- \(T=-\det([\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3])\)
-
求摄像机定向和内部参数:在有限摄像机的情形:
\[ P=[M|-M\tilde{\mathbf{C}}]=K[R|-R\tilde{\mathbf{C}}] \\ K= \begin{bmatrix} \alpha_x & s & x_0 \\ 0 & \alpha_y & y_0 \\ 0 & 0 & 1 \end{bmatrix} \]- \(\alpha_x\) 是 \(x-\) 坐标方向的比例因子
- \(\alpha_y\) 是 \(y-\) 坐标方向的比例因子
- \(s\) 是扭曲参数
- \((x_0,y_0)^\top\) 是主点的坐标
- 像素长宽比\(\alpha_x/\alpha_y\)
无穷远摄像机 ¶
无穷远摄像机是中心在无穷远平面上的摄像机。无穷选摄像机可以分为仿射摄像机和非仿射摄像机
仿射摄像机 ¶
- 仿射摄像机是矩阵 \(P\) 的最后一行 \(P^{3\top}\) 形如 \((0,0,0,1)\) 的摄像机
-
对于有限射影摄像机:
\[ P_0=KR[I|-\tilde{\mathbf{C}}]=K \begin{bmatrix} \mathbf{r}^{1\top}-\mathbf{r}^{1\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{2\top}-\mathbf{r}^{2\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{3\top}-\mathbf{r}^{3\top}\tilde{\mathbf{C}} \end{bmatrix} \]- 其中 \(\mathbf{r}^{i\top}\) 是旋转矩阵的第 i 行。而数值的 \(d_0=-\mathbf{r}^{3\top}\tilde{\mathbf{C}}\) 是世界原点到摄像机中心在主射线方向上的距离
- 沿主射线跟踪的效果是将矩阵的 \((3,4)\) 元素用世界原点到摄像机中心的深度 \(d_t\) 替代
- 假定使图像大小保持不变的放大因子是 \(k=d_t/d_0\),在时间 \(t\) 所产生的摄像机矩阵是:
\[ P_t=K \begin{bmatrix} d_t/d_0 & & \\ & d_t/d_0 & \\ & & 1 \end{bmatrix} \begin{bmatrix} \mathbf{r}^{1\top}&-\mathbf{r}^{1\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{2\top}&-\mathbf{r}^{2\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{3\top}&d_t \end{bmatrix}= \frac{d_t}{d_0}K \begin{bmatrix} \mathbf{r}^{1\top}&-\mathbf{r}^{1\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{2\top}&-\mathbf{r}^{2\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{3\top}d_0/d_t&d_0 \end{bmatrix} \]- 因子 \(d_t/d_0\) 可以忽略,当 \(d_t\) 趋向无穷大时,该矩阵变成
\[ P_\infty=\lim_{t \to \infty}P_t=K \begin{bmatrix} \mathbf{r}^{1\top}&-\mathbf{r}^{1\top}\tilde{\mathbf{C}} \\ \mathbf{r}^{2\top}&-\mathbf{r}^{2\top}\tilde{\mathbf{C}} \\ \mathbf{0}^\top&d_0 \end{bmatrix} \]
应用仿射摄像机的误差 ¶
- 在过世界原点并垂直子主轴方向的平面上的任何点的图像在这种变焦和运动的复合作用下保持不变。这样的一个点可以记为 \(\mathbf{X}=\begin{bmatrix} \alpha \mathbf{r}^1+\beta \mathbf{r}^2 \\ 1\end{bmatrix}\),因为 \(\mathbf{r}^{3\top}(\alpha \mathbf{r}^1+\beta \mathbf{r}^2)=0\),即 \(P_0\mathbf{X}=P_t\mathbf{X}=P_\infty\mathbf{X}\) 对所有 \(t\) 成立
-
对不在该平面上的点,设一点 \(\mathbf{X}\) 离该平面的垂直距离是 \(\Delta\)
- 这个 3D 点可以表示成
\[\mathbf{X}=\begin{bmatrix} \alpha \mathbf{r}^1+\beta \mathbf{r}^2 + \Delta\mathbf{r}^3 \\ 1\end{bmatrix}\]- 并分别被摄像机 \(P_0\) 和 \(P_\infty\) 影像到
\[ \mathbf{x}_{proj}=P_0\mathbf{X}=K\begin{bmatrix} \tilde{x} \\ \tilde{y} \\ d_0+\Delta \end{bmatrix} \ \ \ \mathbf{x}_{affine}=P_\infty\mathbf{X}=K\begin{bmatrix} \tilde{x} \\ \tilde{y} \\ d_0 \end{bmatrix} \]- 其中 \(\tilde{x}=\alpha-\mathbf{r}^{1\top}\tilde{\mathbf{C}},\tilde{y}=\beta-\mathbf{r}^{2\top}\tilde{\mathbf{C}}\),记标定矩阵为:
\[ K=\begin{bmatrix} K_{2 \times 2} & \tilde{\mathbf{x}}_0 \\ \tilde{\mathbf{0}}^\top & 1 \end{bmatrix} \]- 因此两点之间的关系是
\[ \tilde{\mathbf{x}}_{affine}-\tilde{\mathbf{x}}_0= \frac{d_0+\Delta}{d_0}(\tilde{\mathbf{x}}_{proj}-\tilde{\mathbf{x}}_0) \]- 用 \(P_\infty\) 仿射近似真实摄像机矩阵 \(P_0\) 的效应是把点 \(\mathbf{X}\) 的图像径向地靠近或离开主点 \(\tilde{\mathbf{x}}_0\),其加权因子是 \((d_0+\Delta)/d_0=1+\Delta/d_0\)
-
仿射影像条件
\[ \tilde{\mathbf{x}}_{affine}-\tilde{\mathbf{x}}_{proj}=\frac{\Delta}{d_0}(\tilde{\mathbf{x}}_{proj}-\tilde{\mathbf{x}}_0) \]- 深度的起伏 (\(\Delta\)) 相对平均深度 (\(d_0\)) 较小
- 点离主轴的距离较小
\(P_\infty\) 的分解 ¶
- 摄像机矩阵:
\[
P_\infty=
\begin{bmatrix}
K_{2 \times 2} & \hat{\mathbf{0}} \\
\hat{\mathbf{0}}^\top & 1
\end{bmatrix}
\begin{bmatrix}
\hat{R} & \hat{\mathbf{t}} \\
\mathbf{0}^\top & 1
\end{bmatrix}=
\begin{bmatrix}
K_{2 \times 2} & \tilde{\mathbf{x}}_0 \\
\hat{\mathbf{0}}^\top & 1
\end{bmatrix}
\begin{bmatrix}
\hat{R} & \hat{\mathbf{0}} \\
\mathbf{0}^\top & 1
\end{bmatrix}
\]
- 平行投影
- 平行投影矩阵\(\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&0&1 \end{bmatrix}\) 代替离有限摄像机的规范射影矩阵 \([\mathbf{I}|\mathbf{0}]\)
- 标定矩阵\(\begin{bmatrix}K_{2 \times 2} & \hat{\mathbf{0}} \\\hat{\mathbf{0}}^\top & 1\end{bmatrix}\) 代替了有限摄像机的 \(K\)
- 主点无定义
仿射摄像机的层次 ¶
- 正投影:正投影摄像机有 5 个自由度,即描述旋转矩阵 \(R\) 的三个参数,加上两个偏置参数 \(t_1\) 和 \(t_2\)
\[
P=
\begin{bmatrix}
\mathbf{r}^{1\top} & t_1 \\
\mathbf{r}^{2\top} & t_2 \\
\mathbf{0}^\top & 1
\end{bmatrix}
\]
- 缩放正投影:缩放正投影是正投影紧接一个均匀缩放,有 6 个自由度
\[
P=
\begin{bmatrix}
\mathbf{r}^{1\top} & t_1 \\
\mathbf{r}^{2\top} & t_2 \\
\mathbf{0}^\top & 1/k
\end{bmatrix}
\]
- 弱透视投影:与有限 CCD 摄像机类似,考虑两根图像轴缩放因子不一样的无穷远摄像机,有 7 个自由度
\[
P=
\begin{bmatrix}
\alpha_x & & \\
& \alpha_y & \\
& & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{r}^{1\top} & t_1 \\
\mathbf{r}^{2\top} & t_2 \\
\mathbf{0}^\top & 1
\end{bmatrix}
\]
- 仿射摄像机 \(P_A\):如 \(P_\infty\) 一样,可以认为是有限射影摄像机的平行投影,有 8 个自由度
\[
P_A=
\begin{bmatrix}
\alpha_x & s & \\
& \alpha_y & \\
& & 1
\end{bmatrix}
\begin{bmatrix}
\mathbf{r}^{1\top} & t_1 \\
\mathbf{r}^{2\top} & t_2 \\
\mathbf{0}^\top & 1
\end{bmatrix}
\]
仿射摄像机的其他性质 ¶
- 主平面是无穷远平面的任何射影摄像机矩阵是仿射摄像机矩阵
- 平行的世界直线被投影成平行的图像直线
- 满足 \(M_{2 \times 3} \mathbf{d}=\mathbf{0}\) 的矢量 \(\mathbf{d}\) 是平行投影的方向,而 \((\mathbf{d}^\top,0)^\top\) 是摄像机中心,因为 \(P_A\begin{bmatrix} \mathbf{d} \\ 0 \end{bmatrix}=\mathbf{0}\)
一般无穷远摄像机 ¶
| 仿射摄像机 | 非仿射摄像机 | |
|---|---|---|
| 摄像机中心在 \(\pi_\infty\) 上 | 是 | 是 |
| 主平面是 \(\pi_\infty\) | 是 | 不是 |
| \(\pi_\infty\) 的点的图像在 \(\mathbf{l}_\infty\) 上 | 是 | 一般不是 |
其他摄像机模型 ¶
- 推扫式摄像机
- 线阵摄像机