最优化问题 ¶

Abstract

追求最优目标的数学问题都属于最优化问题。

作为最优化问题，至少有两个要素：第一个是可能的方案；第二个是追求的目标。

经典极值问题 ¶

在高数里的微积分中早以涉及到最简单的最优化问题，就是函数极值问题。

可以引申出两种经典最优化的两种类型问题。

无约束极值问题 ¶

\[ \min{f(x_1, x_2, ..., x_n)} \ 或 \ \max{f(x_1, x_2, ..., x_n)} \]

这里的 $f(x_1, x_2, ..., x_n)$ 是定义在 $n$ 维空间上的可微函数。

求极值点方法：从如下的含有 $n$ 个未知数 $x_1, x_2, ..., x_n$ 的非线性方程组中解出驻点，然后判定或验证这些驻点是不是极值点：

\[ f_{x_1}^\prime(x_1, x_2, ..., x_n) = 0 \\ f_{x_2}^\prime(x_1, x_2, ..., x_n) = 0 \\ ... \\ f_{x_n}^\prime(x_1, x_2, ..., x_n) = 0 \]

具有等式约束的极值问题 ¶

\[ \min{f(x_1, x_2, ..., x_n)} \ 或 \ \max{f(x_1, x_2, ..., x_n)} \\ 满足于 \ \ \ h_i(x_1, x_2, ... , x_n) = 0 \ \ j = 1,2,...,l(j < n) \]

求极值点方法：通常采用 $Lagrange$ 乘子法来求解。即把这个问题转换为求 $Lagrange$ 函数的无约束极值问题：

\[ L(x_1, x_2, ... , x_n, \lambda_1, \lambda_2, ..., \lambda_l) \\ = f(x_1, x_2, ..., x_n) - \sum_{j=1}^l \lambda_j h_j(x_1, x_2, ..., x_n) \]

基本概念 ¶

向量表达法 ¶

将 $(x_1, x_2, ..., x_n)$ 看作是 $n$ 维向量空间 $R^n$ 中一个向量 $\mathbf{x}$ 的 $n$ 个分量，即 $\mathbf{x} = (x_1, x_2, ..., x_n)^{\top}$

所以重定义一下最优化问题：

无约束极值问题：

\[\min{f(\mathbf{x})}\]
具有等式约束的极值问题：

\[ \min{f(\mathbf{x})} \\ s.t. \ \ \ \mathbf{h}(\mathbf{x}) = \mathbf{0} \\ 其中 \ \ \ \mathbf{h}(\mathbf{x}) = (h_1(\mathbf{x}), h_2(\mathbf{x}), ..., h_l(\mathbf{x}))^{\top} \]

一般形式 ¶

大部分所要讨论的问题是如下的（静态）最优化问题：

\[ \min_{x \in \Omega}{f(\mathbf{x})} \\ s.t. \ \ \ s_i(\mathbf{x}) \ge 0 \ \ \ i = 1, 2, ..., m \\ h_j(\mathbf{x}) = 0 \ \ \ j = 1, 2, .., l \ (l < n) \]

向量表示法写成：

\[ \min_{x \in \Omega}{f(\mathbf{x})} \\ s.t. \ \ \ \mathbf{s}(\mathbf{x}) \ge \mathbf{0} \\ \mathbf{h}(x) = \mathbf{0} \\ 其中 \ \ \ \mathbf{s}(\mathbf(x)) = (s_1(\mathbf{x}), ..., s_m(\mathbf{x}))^{\top} \]

这种问题称为非线性规划，比具有等式约束的极值问题仅多出 $m$ 个不等式约束。但是，所谓经典问题与近代问题的界限也就在这里。

一些术语
- 满足所有约束的向量 $\mathbf{x}$ 称为容许解或容许点。容许点的集合称为容许集。
- $\mathbf{x}^*$ 称为问题的最优点，而相应的目标函数值 $f(\mathbf{x}^*)$ 称为最优值，$(\mathbf{x}^*, f(\mathbf{x}^*))$ 称为最优解。

分类 ¶

\[ 最优化问题 \left\{\begin{matrix} 静态问题 \left\{\begin{matrix} 无约束问题 \left\{\begin{matrix} 一维问题 \\ n维问题 \end{matrix}\right. \\ 约束问题 \left\{\begin{matrix} 线性规划 \\ 非线性规划 \end{matrix}\right. \end{matrix}\right. \\ 动态问题 \end{matrix}\right. \]

二维问题的图解法 ¶

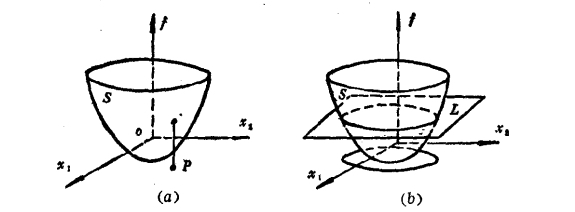
等值线 ¶

用平面 $L$ 去截曲面 $S$ 得到的是一个圆，这个圆又一个重要的性质：圆上任何一点的目标函数都等于 $f_0$。像这样的曲线，其上任何一点的目标函数值都等于同一常数，称为目标函数的等值线。

图解法

\[ 求解\min{(x_1-2)^2+(x_2-1)^2} \\ s.t. \ \ \ x_1+x_2-5=0 \]

先画出目标函数的等值线，再画出约束曲线。实际上约束曲线是一条直线，这条直线就是容许集。因为最优点是容许集上使得等值线具有最小值的点，由下左图可以看出，约束直线与等值线（圆）的切点正是最优点。利用解析几何的有关方法可求的该点是 $\mathbf{x}^x=(3,2)^{\top}$，它所对应的最优值是 $f(\mathbf{x}^*)=2$。

将无约束问题和约束问题的几何图形合在一起，如下右图所示。

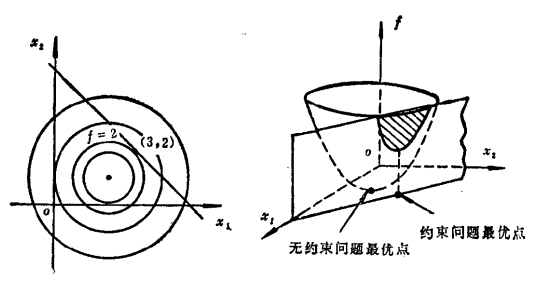
对于二维最优化问题，可以用图解法求解。

等值面 ¶

对于三维及以上的空间，使目标函数取同一常数值的点集 $\{ \mathbf{x} | f(\mathbf{x})= \gamma , \gamma是常数 \}$ 称为等值面。具有一下性质：

有不同值的等值面之间不相交。
除里极值点所在的等值面以外，不会在区域的内部中断。
等值面稠密的地方，目标函数值变化得比较快；稀疏的地方变化得比较慢。
在极值点附近，等值面（线）近似地呈现为同心椭球面族。

二次函数 ¶

在 $n$ 元目标函数中，除里线性函数，最简单最重要的一类就是二次函数。

一般形式是

\[ f(x_1, x_2, ..., x_n)=\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^m q_{ij}x_ix_j+\sum_{i=1}^nb_ix_i+c \]

矩阵形式是

\[ f(\mathbf{x})=\frac{1}{2}\mathbf{x}^{\top}\mathbf{Q}\mathbf{x}+\mathbf{b}^{\top}\mathbf{x}+c \\ 其中 \ \ \ \mathbf{Q} = \begin{bmatrix} q_{11} & q_{12} & ... & q_{1n} \\ q_{21} & q_{22} & ... & q_{2n} \\ ... & ... & ... & ... \\ q_{n1} & q_{n2} & ... & q_{nn} \end{bmatrix} , \ \ \mathbf{b} = \begin{bmatrix} b_1 \\ b_2 \\ ... \\ b_n \end{bmatrix} \]

这里 $\mathbf{Q}$ 是对称矩阵（二次型）。

梯度与 Hesse 矩阵 ¶

梯度 ¶

定义 ¶

函数 $f(\mathbf{x})$ 在 $\mathbf{x}_0$ 处可微

\[ f(\mathbf{x}_0 + \mathbf{p})-f(\mathbf{x}_0) = \mathbf{l}^{\top}\mathbf{p} + o(||\mathbf{p}||) \]

若 $f(\mathbf{x})$ 在 $\mathbf{x}_0$ 处可微，则 $f(\mathbf{x})$ 在该点关于各变量的一阶偏导数存在，并且

\[ \mathbf{l} = (\frac{\partial f(\mathbf{x}_0)}{\partial x_1}, \frac{\partial f(\mathbf{x}_0)}{\partial x_2}, ..., \frac{\partial f(\mathbf{x}_0)}{\partial x_n})^{\top} \]

以 $f(\mathbf{x})$ 的 $n$ 个偏导数为分量的向量称为 $f(\mathbf{x})$ 在 $\mathbf{x}$ 处的梯度

\[ \bigtriangledown f(\mathbf{x}) = (\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, ..., \frac{\partial f(\mathbf{x})}{\partial x_n})^{\top} \]

性质 ¶

过点 $\mathbf{x}_0$ 的等值面方程为 $f(\mathbf{x}) = f(\mathbf{x}_0) 或 f(x_1, x_2, ..., x_n) = \gamma_0 \ \ \ 其中 \ \gamma_0 = f(\mathbf{x}_0)$。
设 $f: R^n \to R^1$ 在点 $\mathbf{x}_0$ 处可微，$\mathbf{p}$ 是固定不变的向量，$\mathbf{e}$ 是方向 $\mathbf{p}$ 上的单位向量，则称极限 $\frac{\partial f(\mathbf{x}_0)}{\partial \mathbf{p}} = \lim_{t \to 0^+} \frac{f(\mathbf{x}_0+t\mathbf{e})-f(\mathbf{x}_0)}{t}$ 为函数 $f(\mathbf{x})$ 在点 $\mathbf{x}_0$ 处沿 $\mathbf{p}$ 方向的方向导数。
设 $f:R^n \to R^1$ 在点 $\mathbf{x}_0$ 处可微，则 $\frac{\partial f(\mathbf{x}_0)}{\partial \mathbf{p}} = \bigtriangledown f(\mathbf{x}_0)^{\top}\mathbf{e}$。其中 $\mathbf{e}$ 是 $\mathbf{p}$ 方向上的单位向量。

特殊类型函数的梯度 ¶

若 $f(\mathbf{x})=C$( 常数 )，则 $\bigtriangledown f(\mathbf{x})=\mathbf{0}$，即 $\bigtriangledown C = \mathbf{0}$
$\bigtriangledown (\mathbf{b}^{\top}\mathbf{x})=\mathbf{b}$
$\bigtriangledown (\mathbf{x}^{\top}\mathbf{x})=2\mathbf{x}$
若 $\mathbf{Q}$ 是对称方阵，则 $\bigtriangledown (\mathbf{x}^{\top}\mathbf{Q}\mathbf{x})=2\mathbf{Q}\mathbf{x}$

Hesse 矩阵 ¶

多元函数 $f(\mathbf{x})$ 的一阶导数是它的梯度 $\bigtriangledown f(\mathbf{x})$，二阶导数是它的 Hesse 矩阵 $\bigtriangledown^2f(\mathbf{x})$。

\[ \bigtriangledown^2 f(\mathbf{x})=\bigtriangledown(\bigtriangledown f(\mathbf{x}))= \begin{bmatrix} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2 \partial x_1} & ... & \frac{\partial^2 f(\mathbf{x})}{\partial x_n \partial x_1} \\ \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} & ... & \frac{\partial^2 f(\mathbf{x})}{\partial x_n \partial x_2} \\ ... & ... & ... & ... \\ \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_n} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2 \partial x_n} & ... & \frac{\partial^2 f(\mathbf{x})}{\partial x_n^2} \\ \end{bmatrix} \]

常用公式：
1. $\bigtriangledown \mathbf{c}=\mathbf{O}$，其中 $\mathbf{c}$ 是分量全为常数的 $n$ 维向量，$\mathbf{O}$ 是 $n \times n$ 阶零矩阵。
2. $\bigtriangledown \mathbf{x} = \mathbf{I}$，其中 $\mathbf{x}$ 是 $n$ 维向量，$\mathbf{I}$ 是 $n \times n$ 阶单位矩阵。
3. $\bigtriangledown (\mathbf{Q}\mathbf{x})=\mathbf{Q}$，其中 $\mathbf{Q}$ 是 $n \times n$ 阶矩阵。
4. 设 $\varphi (t)=f(\mathbf{x}_0 + t\mathbf{p})$，其中 $f:R^n \to R^1, \varphi: R^{\top} \to R^1$，则
\[ \varphi^\prime(t)=\bigtriangledown f(\mathbf{x}_0 + t\mathbf{p})^{\top}\mathbf{p} \\ \varphi^{\prime \prime}(t)=\mathbf{p}^{\top}\bigtriangledown^2f(\mathbf{x}_0+t\mathbf{p})\mathbf{p} \]

多元函数的 Taylor 展开式 ¶

设 $f:R^n \to R^1$ 具有二阶连续偏导数，则

\[ f(\mathbf{x}+\mathbf{p})=f(\mathbf{x})+\bigtriangledown f(\mathbf{x})^{\top}\mathbf{p}+\frac{1}{2}\mathbf{p}^{\top}\bigtriangledown^2f(\bar{\mathbf{x}})\mathbf{p} \\ 其中\bar{\mathbf{x}}=\mathbf{x}+\theta \mathbf{p}，而0 < \theta < 1 \]

凸集与凸函数 ¶

凸集 ¶

设 $x_1, x_2, ..., x_l$ 是 $R^n$ 中的 $l$ 个已知点。若对某点 $x \in R^n$ 存在常数 $a_1, a_2, ..., a_l \ge 0$ 且 $\sum_{i=1}^la_i=1$ 使得 $x=\sum_{i=1}^la_ix_i$，则称 $x$ 是 $x_1, x_2,...,x_l$ 的凸组合。若 $a_1, a_2, ..., a_l > 0$ 且 $\sum_{i=1}^la_i=1$，则称 $x$ 是 $x_1, x_2, ..., x_l$ 的严格凸组合。
设集合 $C \subseteq R^n$，如果对于任意两点 $x_1, x_2 \in C$，它们的任意凸组合仍然属于 C，那么称集合 C 为凸集。
设集合 $\alpha \in R^n$ 且 $\alpha \ne 0, b \in R^1$，则集合 $\{x | \alpha^{\top}x=b,x \in R^n\}$ 称为 $R^n$ 中的超平面，$\alpha$ 称为这个超平面的法向量。
设集合 $\alpha \in R^n$ 且 $\alpha \ne 0, b \in R^1$，则集合 $\{x | \alpha^{\top}x=b,x \in R^n\}$ 称为 $R^n$ 中的半空间。
任意一组凸集的交仍然是凸集。

凸函数 ¶

设 $f: C \subseteq R^n \to R^1$，其中 C 为凸集。若对于任意两点 $x_1, x_2 \in C$ 和任意一对满足 $\alpha_1 + \alpha_2 = 1$ 的数 $\alpha_1, \alpha_2 \in [0,1]$ 都有 $f(\alpha_1x_1+\alpha_2x_2) \le \alpha_1f(x_1)+\alpha_2f(x_2)$，则称 f 为定义在凸集 C 上的凸函数（严格小于时为严格凸函数）
若函数 f 在凸集 C 上是（严格）凸函数，则称 f 是定义在凸集 C 上的（严格）凸函数。
设 $f: C \subset R^n \to R^1$，其中 C 为非空凸集。若 f 是凸函数，则对于任意实数 $\beta$，水平集 $D_\beta = \{x | f(x) \le \beta, x \in C\}$ 是凸集。
设 $f: C \subseteq R^n \to R^1$，其中 C 是非空凸集，f 是凸函数，则形式为 $\min f(x) \ s.t. \ x \in C$ 的问题称为凸规划。
设 $x^\prime$ 是凸规划的局部极小点
- 若 f 是凸函数，则 $x^\prime$ 是全局极小点
- 若 f 是严格凸函数，则 $x^\prime$ 是唯一全局最小点
设 $f:C \subseteq R^n \to R^1$ 是可微函数，其中 C 为凸集，则
- f 为凸函数的充要条件是，$\forall x_1, x_2 \in C$ 都有 $f(x_2) \ge f(x_1) + $\bigtriangledown f(x_1)^{\top}(x_2-x_1)$
- f 是严格凸函数的充要条件是，$\forall x_1, x_2 \in C$ 且 $x_1 \ne x_2$ 都有 $f(x_2) > f(x_1) + \bigtriangledown f(x_1)^{\top}(x_2-x_1)$
设 $f:C \subseteq R^n \to R^1$ 是二次可微函数，C 为非空开凸集，则 f 为 C 上凸函数的充要条件是， Hesse 矩阵 $\bigtriangledown^2 f(x)$ 在 C 上到处半正定（满足半正定时，则 f 在 C 上为严格凸函数）。

极小点的判定条件 ¶

设 $f:D \subseteq R^n \to R^1$ 具有连续的一阶偏导数。若 $x^\prime$ 是 $f(x)$ 的局部极小点并且是 D 的内点，则 $\bigtriangledown f(x^\prime) = 0$
设 $f:D \subseteq R^n \to R^1$，$x^\prime$ 是 D 的哪点。若 $\bigtriangledown f(x^\prime) = 0$，则 $x^\prime$ 称为 $f(x)$ 的驻点。
设 $f:D \subseteq R^n \to R^1$ 具有连续的二阶偏导数，$x^\prime$ 是 D 的一个内点。若 $\bigtriangledown f(x^\prime)=0$ 并且 $\bigtriangledown^2 f(x^\prime)$ 是正定的，则 $x^\prime$ 是 $f(x)$ 的严格局部极小点。

下降迭代算法 ¶

给定初始点后，如果每迭代一步都使目标函数有所下降，即 $f(\mathbf{x}_{k+1}) < f(\mathbf{x}_k)$，那这种迭代法称为下降法。

在迭代过程中有两个规则需要确定，一个是下降方向 $\mathbf{p}_k$ 的选取；一个是步长因子 $t_k$ 的选取。

算法的基本格式如下：

选取初始点 $\mathbf{x}_0$，置 $k=0$
按某种规则确定 $\mathbf{p}_k$ 使得 $\bigtriangledown f(\mathbf{x}_k)^{\top} \mathbf{p}_k < 0$
按某种规则确定 $t_k$ 使得 $f(\mathbf{x}_k+t_k\mathbf{p}_k)<f(\mathbf{x}_k)$
计算 $\mathbf{x}_{k+1}=\mathbf{x}_k+t_k\mathbf{p}_k$
判定 $\mathbf{x}_{k+1}$ 时候满足终止准则，若满足，打印 $\mathbf{x}_{k+1}$ 和 $f(\mathbf{x}_{k+1})$，停机；否则置 $k=k+1$，转 2

最后更新: 2025年5月9日 15:51:31
创建日期: 2023年8月26日 15:00:56