3D 射影几何和变换¶

约 2831 个字 2 张图片预计阅读时间 9 分钟

Abstract

本章主要介绍 3 维射影空间\(IP^3\)的性质和基本要素。

点和射影变换¶

三维空间的一点 \(\mathbf{X}\) 用齐次坐标表示为一个 4 维矢量，齐次矢量 \(\mathbf{X}=(X_1,X_2,X_3,X_4)^{\top}\)当\(X_4 \ne 0\)时表示为\(IR^3\)中非齐次坐标为\((X,Y,Z)^{\top}\)的点，其中 \(\mathbf{X}=X_1/X_4,Y=X_2/X_4,Z=X_3/X_4\)。
当\(X_4=0\)的齐次点表示无穷远点。
\(IR^3\)上的射影变换是由非奇异\(4 \times 4\)矩阵给出，它是关于齐次 4 维矢量的线性变换：\(\mathbf{X}^\prime=H\mathbf{X}\)，该映射是保线变换（直线被映射到直线）。

平面、直线和二次曲面的表示和变换¶

平面¶

平面的齐次表示为\(\mathbf{\pi}=(\pi_1, \pi_2, \pi_3, \pi_4)^{\top}\)。
点\(\mathbf{X}\)在平面\(\mathbf{\pi}\)上则：\(\mathbf{\pi}^{\top}\mathbf{X}=0\)
联合与关联关系
- 平面可由一般位置的三个点或一条直线与一个点的联合来唯一确定（一般位置指三点不共线或在后一种情形下指点不在直线上）
- 两张不同的平面相交于唯一的直线
- 三张不同的平面相交于唯一的点
三点确定一张平面
- 确定平面的三个点是\(\mathbf{X}_1=(\hat{\mathbf{X}_1})^{\top}、\mathbf{X}_2=(\hat{\mathbf{X}_2})^{\top}、\mathbf{X}_3=(\hat{\mathbf{X}_3})^{\top}\)，则
\[ \mathbf{\pi}=((\hat{\mathbf{X}_1}-\hat{\mathbf{X}_3}) \times (\hat{\mathbf{X}_2}-\hat{\mathbf{X}_3}), -\hat{\mathbf{X}_3}^{\top}(\hat{\mathbf{X}_1} \times \hat{\mathbf{X}_2}))^{\top} \]
三平面确定一点
- 三平面\(\mathbf{\pi}_i\)的交点\(\mathbf{X}\)可通过求以三张平面为行的\(3 \times 4\)矩阵的（右）零空间直接计算出来：
\[ \begin{bmatrix} \mathbf{\pi}_1^{\top}\\ \mathbf{\pi}_2^{\top}\\ \mathbf{\pi}_3^{\top} \end{bmatrix} \mathbf{X}=\mathbf{0} \]
射影变换
- 在点变换\(\mathbf{X}^\prime=H\mathbf{X}\)下，平面变换为\(\mathbf{\pi}^\prime=H^{-\top}\mathbf{\pi}\)
平面上的点的参数表示
- 在平面\(\mathbf{\pi}\)上的点\(\mathbf{X}\)可以写成\(\mathbf{X}=M\mathbf{x}\)
- 其中\(4 \times 3\)矩阵\(M\)的列生成\(\mathbf{\pi}^{\top}\)的秩为 3 的零空间，即\(\mathbf{\pi}^{\top} M=\mathbf{0}^{\top}\)

直线¶

零空间
- 一个算子\(\mathbf{A}\)的零空间是\(\mathbf{A}\mathbf{v}=\mathbf{0}\)的所有解\(\mathbf{v}\)的集合。它也叫做\(\mathbf{A}\)的核，核空间。如果算子是在向量空间上的线性算子，零空间就是线性子空间。因此零空间也是向量空间。
生成子空间
- 设\(\alpha_1, \alpha_2, ..., \alpha_m\)是\(R^m\)中任一组向量。记\(\alpha_1, \alpha_2, ..., \alpha_m\)的所有线性组合的集合为\(span(\alpha_1, \alpha_2, ..., \alpha_m)\)，即\(span(\alpha_1, \alpha_2, ..., \alpha_m)=\{k_1\alpha_1+k_2\alpha_2+...+k_m\alpha_m | k_i \in R, i=1,2,...,m\}\)，称\(span(\alpha_1, \alpha_2, ..., \alpha_m)\)为向量组\(\alpha_1, \alpha_2, ..., \alpha_m\)生成的子空间。
零空间与生成子空间表示
- 假定\(\mathbf{A}、\mathbf{B}\)是两（不重合）的空间点，那么连接这两点的直线由一个\(2 \times 4\)矩阵\(W\)的行的生成子空间表示，\(W=\begin{bmatrix} \mathbf{A}^{\top} \\ \mathbf{B}^{\top} \end{bmatrix}\)
  - \(W^{\top}\)的生成子空间是在直线\(\lambda \mathbf{A}+\mu \mathbf{B}\)上的点束
  - \(W\)的 2 维右零空间的生成子空间是以直线为轴的平面束
- 一条直线的对偶表示是两平面\(\mathbf{P}，\mathbf{Q}\)的交线，该直线表示为矩阵\(W^*=\begin{bmatrix} \mathbf{P}^{\top} \\ \mathbf{Q}^{\top} \end{bmatrix}\)
  - \(W^{*\top}\)的生成子空间是以该直线为轴的平面束\(\lambda^\prime\mathbf{P}+\mu^\prime\mathbf{Q}\)
  - \(W^{*\top}\)的 2 维零空间的生成子空间是该直线上的点束
- 这两种表示以\(W^*W^{\top}=WW^{*\top}=0_{2\times 2}\)相联系
Plücker 矩阵
- 这里一条直线由\(4 \times 4\)反对称齐次矩阵表示。连接两点\(\mathbf{A}, \mathbf{B}\)的直线由矩阵\(\mathbf{L}\)表示，其元素为：\(l_{ij}=A_iB_j-B_iA_j\)，或用矢量记号等价于表示为\(L=\mathbf{A}\mathbf{B}^{\top}-\mathbf{B}\mathbf{A}^{\top}\)
- 性质
  - \(L\)的秩为 2
  - 该表示具有描述一条直线所需要的 4 个自由度
  - 矩阵\(L\)与用来确定它的点\(\mathbf{A}, \mathbf{B}\)无关
  - 在点变换\(\mathbf{X}^\prime=H\mathbf{X}\)下，该矩阵变换为\(L^\prime=HLH^{\top}\)时，即它是一个阶为 2 的张量
    - 由两平面\(\mathbf{P}, \mathbf{Q}\)的交线确定的直线的对偶 Plücker 表示为\(L^*\)为\(L^*=\mathbf{P}\mathbf{Q}^{\top}-\mathbf{Q}\mathbf{P}^{\top}\)
    - 由点\(\mathbf{X}\)和直线\(L\)联合而确定的平面为\(\mathbf{\pi}=L^*\mathbf{X}\)，并且\(L^*\mathbf{X}=0\)的充要条件是\(\mathbf{X}\)在\(L\)上
    - 由直线\(L\)和平面\(\mathbf{\pi}\)相交而确定的点为\(\mathbf{X}=L\mathbf{\pi}\)，并且\(L\mathbf{\pi}=\mathbf{0}\)的充要条件是\(L\)在\(\mathbf{\pi}\)上
Plücker 直线坐标
- Plücker 直线坐标是\(4 \times 4\)反对称 Plücker 矩阵\(L\)的六个非零元素，即\(\mathcal{L}=\{l_{12},l_{13},l_{14},l_{23},l_{42},l_{34}\}\)
- 由于\(\det{L}=0\)，所以坐标满足\(l_{12}l_{34}+l_{13}l_{42}+l_{14}l_{23}=0\)
- 两条直线\(\mathcal{L}\)和\(\hat{\mathcal{L}}\)共面（因而相交）的充要条件是\((\mathcal{L} | \hat{\mathcal{L}})=0\)
  - 如果\((\mathcal{L} | \hat{\mathcal{L}})=0\)，则 6 维矢量\(\mathcal{L}\)仅表示\(IP^3\)中的一条直线
  - 假定两条直线\(\mathcal{L}, \hat{\mathcal{L}}\)分别为平面\(\mathbf{P}, \mathbf{Q}\)和\(\hat{\mathbf{P}}, \hat{\mathbf{Q}}\)的交线，那么\((\mathcal{L} | \hat{\mathcal{L}})=\det [\mathbf{P}, \mathbf{Q}, \hat{\mathbf{P}}, \hat{\mathbf{Q}}]\)，同理，两条直线相交的充要条件就是\((\mathcal{L} | \hat{\mathcal{L}})=0\)
  - 如果\(\mathcal{L}\)是两平面\(\mathbf{P}, \mathbf{Q}\)的交线，而\(\hat{\mathcal{L}}\)是两点\(\mathbf{A}, \mathbf{B}\)的连线，那么\((\mathcal{L} | \hat{\mathcal{L}})=(\mathbf{P}^{\top}\mathbf{A})(\mathbf{Q}^{\top}\mathbf{B})-(\mathbf{Q}^{\top}\mathbf{A})(\mathbf{P}^{\top}\mathbf{B})\)

二次曲面与对偶二次曲面¶

\(IP^3\)中，二次曲面由下列方程定义：\(\mathbf{X}^{\top} Q\mathbf{X}=0\)，其中\(Q\)是一个\(4 \times 4\)的对称矩阵
个二次曲面有 9 个自由度
一般位置上的九个点确定一个二次曲面
如果矩阵\(Q\)是奇异的，那么二次曲面是退化的，并可以由较少的点来确定
二次曲面定义了点和平面之间的一种配极，类似于二次曲线在点和直线之间定义的配极，平面\(\mathbf{\pi}=Q\mathbf{X}\)称为是\(\mathbf{X}\)关于\(Q\)的极平面，当\(Q\)为非奇异并且\(\mathbf{X}\)在二次曲面之外时，极平面由过\(\mathbf{X}\)且与\(Q\)相切的射线组成的锥与\(Q\)想接触的点来定义。如果\(\mathbf{X}\)在\(Q\)上，那么\(Q\mathbf{X}\)是\(Q\)在点\(\mathbf{X}\)的切平面
平面\(\mathbf{\pi}\)与二次曲面\(Q\)的交线是二次曲线\(C\)
在点变换\(\mathbf{X}^\prime=H\mathbf{X}\)下，（点）二次曲面变换为\(Q^\prime=H^{-\top}QH^{-1}\)

二次曲面的分类¶

对角矩阵\(D\)的符号差，记为\(\sigma(D)\)，定义为\(D\)中 +1 的个数与 -1 的个数的差值

三次绕线¶

三次绕线可以看成 2D 二次曲线的 3 维类推。一条三次绕线定义为\(IP^3\)中的一条曲线，它的参数形式如下：

\[ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = A \begin{bmatrix} 1 \\ \theta \\ \theta^2 \\ \theta^3 \end{bmatrix} = \begin{bmatrix} a_{11}+a_{12}\theta+a_{13}\theta^2+a_{14}\theta^3 \\ a_{21}+a_{22}\theta+a_{23}\theta^2+a_{24}\theta^3 \\ a_{31}+a_{32}\theta+a_{33}\theta^2+a_{34}\theta^3 \\ a_{41}+a_{42}\theta+a_{43}\theta^2+a_{44}\theta^3 \end{bmatrix} \]

性质
- 令\(\mathbf{c}\)为一条非奇异三次绕线。那么\(\mathbf{c}\)不整个地包含在\(IP^3\)的任何一张平面中，而是与一般平面有三个不同的交点
- 三次绕线有 12 个自由度
- 所有非退化的三次绕线都是射影等价的

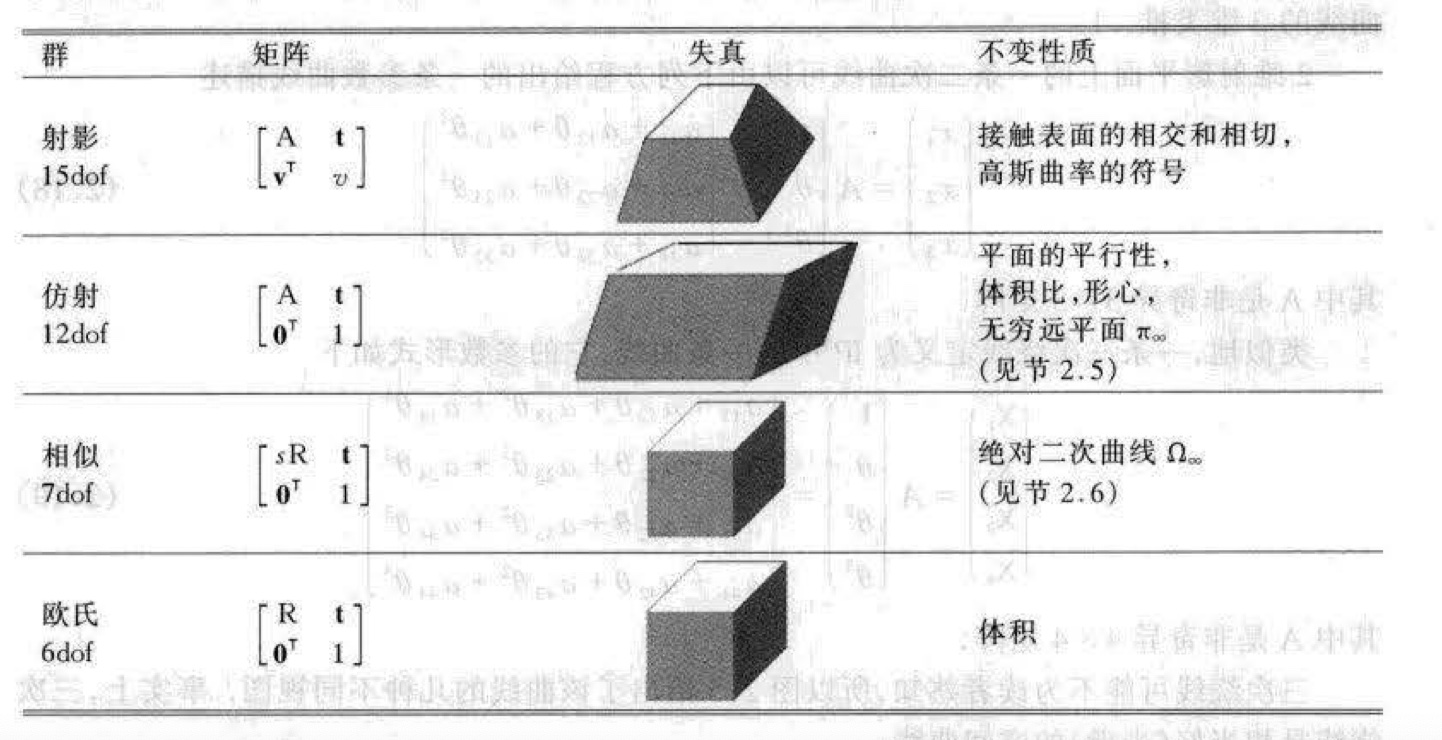
变换的层次¶

3 维空间变换同样具有相应的 2 维空间变换
高斯曲率：微分几何中，曲面上一点的高斯曲率是该点主曲率\(k_1\)和\(k_2\)的乘积。它是曲率的内在度量，也即，它的值只依赖于曲面上的距离如何测量，而不是曲面如何嵌入到空间。
转动分解
- 任何具体的平移加旋转运动都等价于绕一根转动轴的旋转加沿该转动轴的平移。该转动轴平行于原来的旋转轴。
- 平移加绕正交轴的旋转运动(称平面运动)等价于仅仅绕某转动轴的旋转。

无穷远平面¶

在 3 维空间的射影几何中，与\(\mathbf{I}_{\infty}\)的虚圆点对应的几何实体是无穷远平面\(\mathbf{\pi}_{\infty}\)和绝对二次曲线\(\Omega_\infty\)
在 3 维仿射空间中，无穷远平面的标准位置是\(\mathbf{\pi}_\infty=(0,0,0,1)^{\top}\)，\(\mathbf{\pi}_\infty\)包含所有方向\(\mathbf{D}=(X_1,X_2,X_3,0)^{\top}\)并且可以用来识别仿射性质
- 两张平面相平行的充要条件是它们的交线在\(\mathbf{\pi}_\infty\)上
- 如果一条直线与另一条直线或一张平面相交于\(\mathbf{\pi}_\infty\)上，则它们相平行
在射影变换\(H\)下，无穷远平面\(\mathbf{\pi}_\infty\)是不动平面的充要条件是\(H\)是一个仿射变换
- 一般地说，在仿射变换下平面\(\mathbf{\pi}_\infty\)是整个集合不动，而不是点点不动
- 仅有\(\mathbf{\pi}_\infty\)在任何仿射变换下保持不动

绝对二次曲线¶

绝对二次曲线\(\Omega_\infty\)是在\(\pi_\infty\)上一条（点）二次曲线。在度量坐标系中\(\pi_\infty=(0,0,0,1)^{\top}\)，而在\(\Omega_\infty\)上的点满足：\(\left.\begin{matrix} X_1^2+X_2^2+X_3^2 \\ X_4^2 \end{matrix}\right\} = 0\)
在射影变换\(H\)下，绝对二次曲线\(\Omega_\infty\)是不动二次曲线的充要条件是\(H\)是相似变换
- \(\Omega_\infty\)在一般相似变换下是集合不懂，而不是点点不动的
- 所有的圆交\(\Omega_\infty\)于两点，这两点是虚圆点
- 所有球面交\(\pi_\infty\)于\(\Omega_\infty\)
度量性质：一旦\(\Omega_\infty\)在 3 维射影空间被辨认，那么诸如夹角和相对长度等度最性质可以被测定。设两条直线的方向为\(d_1\)和\(d_2\)（3 维矢量），则

\[ \cos \theta = \frac{(\mathbf{d}_1^{\top} \Omega_\infty \mathbf{d}_2)}{(\mathbf{d}_1^{\top} \Omega_\infty \mathbf{d}_1)(\mathbf{d}_2^{\top} \Omega_\infty \mathbf{d}_2)} \]

正交与配极：如果\(\mathbf{d}_1^{\top} \Omega_\infty \mathbf{d}_2=0\)，则\(\mathbf{d}_1\)和\(\mathbf{d}_2\)相垂直。因而垂直性可由关于\(\Omega_\infty\)的共轭性来表征

绝对对偶二次曲面¶

绝对二次曲线\(\Omega_\infty\)的对偶是 3 维空间中一种退化的对偶二次曲面，称为绝对对偶二次曲面并记为\(Q_\infty^*\)。从几何上说，\(Q_\infty^*\)由\(\Omega_\infty\)的切平面组成，它被称为边二次曲面。它在 3 维度量空间的标准形式是：\(Q_\infty^* = \begin{bmatrix} \mathbf{I} & \mathbf{0} \\ \mathbf{0}^{\top} & 0 \end{bmatrix}\)
绝对对偶二次曲面\(Q_\infty^*\)不动的充要条件是\(H\)是相似变换
无穷远平面\(\pi_\infty\)是\(Q_\infty^*\)的零矢量
两张平面\(\pi_1\)和\(\pi_2\)之间的夹角由下式给出：

\[ \cos \theta = \frac{\mathbf{\pi}_1^{\top} Q_\infty^* \mathbf{\pi}_2}{\sqrt{(\mathbf{\pi}_1^{\top} Q_\infty^* \mathbf{\pi}_1)(\mathbf{\pi}_2^{\top} Q_\infty^* \mathbf{\pi}_2)}} \]