算法评价和误差分析 ¶

性能的界定 ¶

• 记号的规定
  • 测量得到的量，如 \(\mathbf{x}\) 表示图像点
  • 被估计的量用加帽子来标识，如 \(\hat{\mathbf{x}}\) 或 \(\hat{H}\)
  • 量的真值用加横杠表示，如 \(\bar{\mathbf{x}}\) 或 \(\bar{H}\)

单图像误差 ¶

• 2D 单应的估计问题在仅给第二幅图像的坐标加噪声的情形下，设有 n 组这样的匹配点， RMS（均方根）残差：

双图像误差 ¶

• 对双图像误差情形，残差是

最优估计算法（MLE）¶

• \(IR^N\) 上总方差为 \(N\delta^2\) 的各向同性高斯分布向一个 \(s\) 维子空间的投影是总方差为 \(s\sigma^2\) 的各向同性高斯分布

• 考虑一个估计问题，其中 \(N\) 个测量由依赖于 \(d\) 个本质参数集的函数模型化。假定每个测量变量有标准差 \(\delta\) 的独立高斯噪声。

  • ML 估计算法的 RMS 残差（测量值到估计值的距离）是
  \[ \varepsilon_{res}=E [\parallel \hat{\mathbf{X}} - \mathbf{X} \parallel / \mathbf{N}]^{1/2}=\sigma(1-d/N)^{1/2} \]
  • ML 估计算法的 RMS 估计误差（估计值到真值的距离）是
  \[ \varepsilon_{est}=E [\parallel \hat{\mathbf{X}} - \bar{\mathbf{X}} \parallel / \mathbf{N}]^{1/2}=\sigma(d/N)^{1/2} \]

变换估计的协方差 ¶

• 求得的变换的不可靠性通常由变换的协方差矩阵获取，因为 \(H\) 是 9 元素的矩阵，它的协方差矩阵是一个 \(9\times 9\) 矩阵。

协方差的前向传播 ¶

• 令 \(\mathbf{v}\) 是 \(IR^M\) 中的一个具有均值 \(\bar{v}\) 和协方差矩阵 \(\sum\) 的随机矢量，假定 \(f:IR^M \to IR^N\) 是一个仿射映射：定义为 \(f(\mathbf{v})=f(\bar{\mathbf{v}})+A(\mathbf{v}-\bar{\mathbf{v}})\)。那么 \(f(\mathbf{v})\) 是一个具有均值 \(f(\bar{\mathbf{v}})\) 和协方差矩阵 \(A\sum A^\top\) 的随机变量。
• 令 \(\mathbf{v}\) 是 \(IR^M\) 中的一个具有均值 \(\bar{\mathbf{v}}\) 和协方差矩阵 \(\sum\) 的随机矢量，假定 \(f:IR^M \to IR^N\) 在 \(\bar{\mathbf{v}}\) 的邻域可微，那么在精确到一阶近似的程度下，\(f(\mathbf{v})\) 是一个具有均值 \(f(\bar{\mathbf{v}})\) 和协方差矩阵 \(J\sum J^\top\) 的随机变量，其中 \(J\) 是 \(f\) 的雅可比矩阵在 \(\bar{\mathbf{v}}\) 的值。

协方差的反向传播 ¶

• 协方差的反向输送——仿射情形：令 \(f:IR^M \to IR^N\) 是形为 \(f(\mathbf{P})=f(\bar{\mathbf{P}}) + J(\mathbf{P}-\bar{\mathbf{P}})\) 的仿射映射，其中 \(J\) 的秩等于 \(M\)。令 \(\mathbf{X}\) 是 \(IR^N\) 中的一个具有均值 \(\bar{\mathbf{X}}=f(\bar{\mathbf{P}})\) 和协方差矩阵 \(\sum\) 的随机变量。令 \(f^{-1} \small\circ \eta:IR^N \to IR^M\) 是一映射，它把测量矢量 \(\mathbf{X}\) 映射到对应于 ML 估计 \(\hat{\mathbf{X}}\) 的参数矢量 \(\mathbf{P}\)，那么 \(\hat{\mathbf{P}}=f^{-1} \small\circ (\mathbf{X})\) 是一个具有均值 \(\bar{\mathbf{P}}\) 的随机变量，其协方差矩阵是

• 协方差的反向输送——非线性情形：令 \(f:IR^M \to IR^N\) 是一个可微映射，而 \(J\) 是它在点 \(\bar{\mathbf{P}}\) 处的雅可比矩阵。假定 \(J\) 的秩为 \(M\)，则 \(f\) 在 \(\bar{\mathbf{P}}\) 的邻域是一一对应的。令 \(\mathbf{X}\) 是 \(IR^N\) 中的一个具有均值 \(\bar{\mathbf{X}}=f(\bar{\mathbf{P}})\) 和协方差矩阵 \(\sum_{\mathbf{x}}\) 的随机变量。令映射 \(f^{-1} \small\circ \eta:IR^N \to IR^M\)，把测量矢量 \(\mathbf{X}\) 映射到对应于 ML 估计 \(\hat{\mathbf{X}}\) 的参数矢量 \(\mathbf{P}\)。那么在一阶精度下，\(\hat{\mathbf{P}}=f^{-1} \small \circ \eta(\mathbf{X})\) 是一个具有均值 \(\bar{\mathbf{P}}\) 和协方差矩阵 \((J^\top \sum_{\mathbf{x}}\nolimits^{-1} J)^{-1}\) 的随机变量。

超参数化 ¶

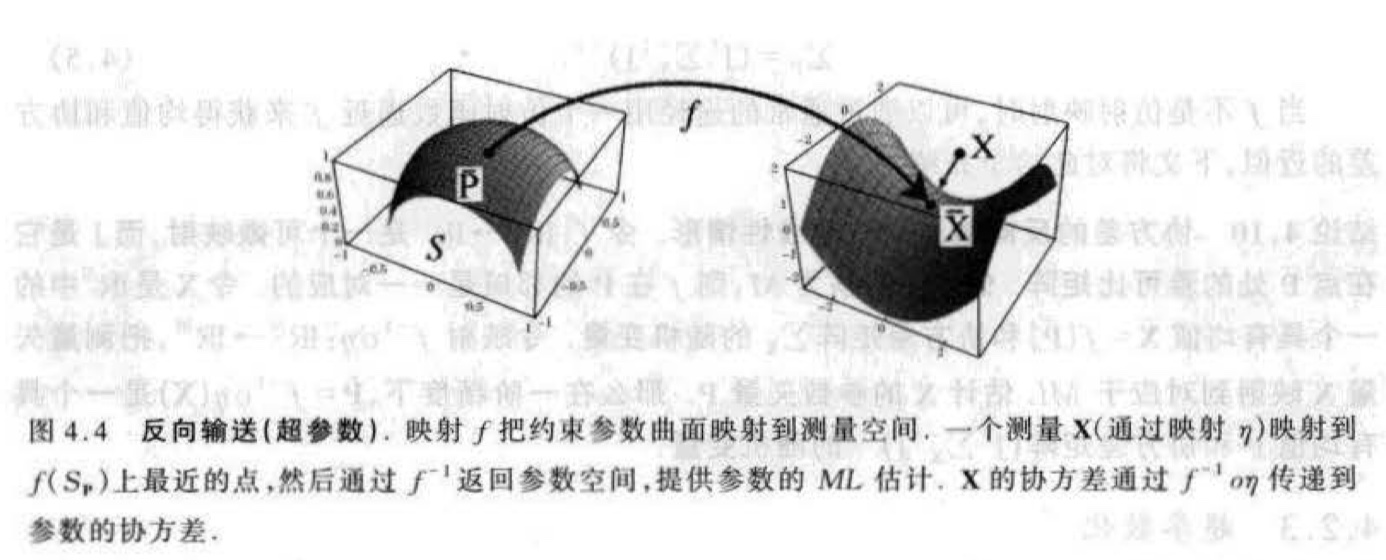
• 协方差的反向输送——超参数化情形。令 \(f:IR^M \to IR^N\) 是一个可微映射，它把一组参数 \(\bar{\mathbf{P}}\) 映射到测量矢量 \(\bar{\mathbf{X}}\)，令 \(S_\mathbf{p}\) 是嵌入 \(IR^M\) 中过点 \(\bar{\mathbf{P}}\) 的 d 维光滑流形并使得映射 \(f\) 在流形 \(S_\mathbf{p}\) 上 \(\bar{\mathbf{P}}\) 的一个邻域内是一一对应的，\(f\) 把 \(S_\mathbf{p}\) 局域地映射到 \(IR^N\) 上到流形 \(f(S_\mathbf{p})\)。函数 \(f\) 有一个局部逆函数，记为 \(f^{-1}\)，它限制在曲面 \(f(S_\mathbf{p})\) 上 \(\bar{\mathbf{X}}\) 的一个邻域内，定义 \(IR^N\) 上的一个具有均值 \(\bar{\mathbf{X}}\) 和协方差 \(\sum_{\mathbf{x}}\) 的高斯分布，并令 \(\eta: IR^N \to f(S_\mathbf{p})\) 把 \(IR^N\) 上的点映射到 \(f(S_\mathbf{p})\) 上并在 Mahalanobis 范数 \(\parallel \cdot \parallel_{\sum_{\mathbf{x}}}\) 意义下最近的点，\(IR^N\) 上具有协方差矩阵 \(\sum_\mathbf{x}\) 的概率分布通过 \(f^{-1} \small\circ \eta\) 诱导 \(IR^M\) 上的概率分布，它在一阶精度下的协方差矩阵是

• 其中 \(A\) 是任意 \(m \times d\) 矩阵，它的列矢量生成 \(S_\mathbf{p}\) 的过点 \(\bar{\mathbf{P}}\) 的切空间。

• 令可微映射 \(f:IR^M \to IR^N\)，把 \(\bar{\mathbf{P}}\) 映射到 \(\bar{\mathbf{X}}\)，并令 \(J\) 为 \(f\) 的雅可比矩阵，设 \(IR^N\) 上一个具有协方差矩阵 \(\sum_{\mathbf{x}}\) 的高斯分布定义在 \(\bar{\mathbf{X}}\)，令 \(f^{-1} \small\circ \eta:IR^N \to IR^M\) 是把一个测量 \(\mathbf{X}\) 映到约束在局部正交于 \(J\) 的零空间的曲面 \(S_\mathbf{p}\) 上的 MLE 参数矢量 \(\mathbf{P}\) 的映射，那么 \(f^{-1} \small\circ \eta\) 诱导在 \(IR^M\) 上的一个分布，它的协方差矩阵在一阶精度下是：

协方差估计的蒙特卡洛法 ¶

• 之前讨论的协方差估计方法都建立在线性假定之上。
• 如果不知道 H 的真值时，估计变换 H 的协方差的解析法和蒙特卡洛法都可以用于实际数据的协方差估计。