单视图几何¶

约 3225 个字 5 张图片预计阅读时间 11 分钟

Abstract

本章主要讨论在透视投影下其他的 3D 几何实体与其 2D 图像之间的联系。
这些实体包括平面、直线、二次曲线、二次曲面，将推导它们的正向和反向投影的性质

射影摄像机对平面、直线和二次曲线的作用¶

对平面的作用¶

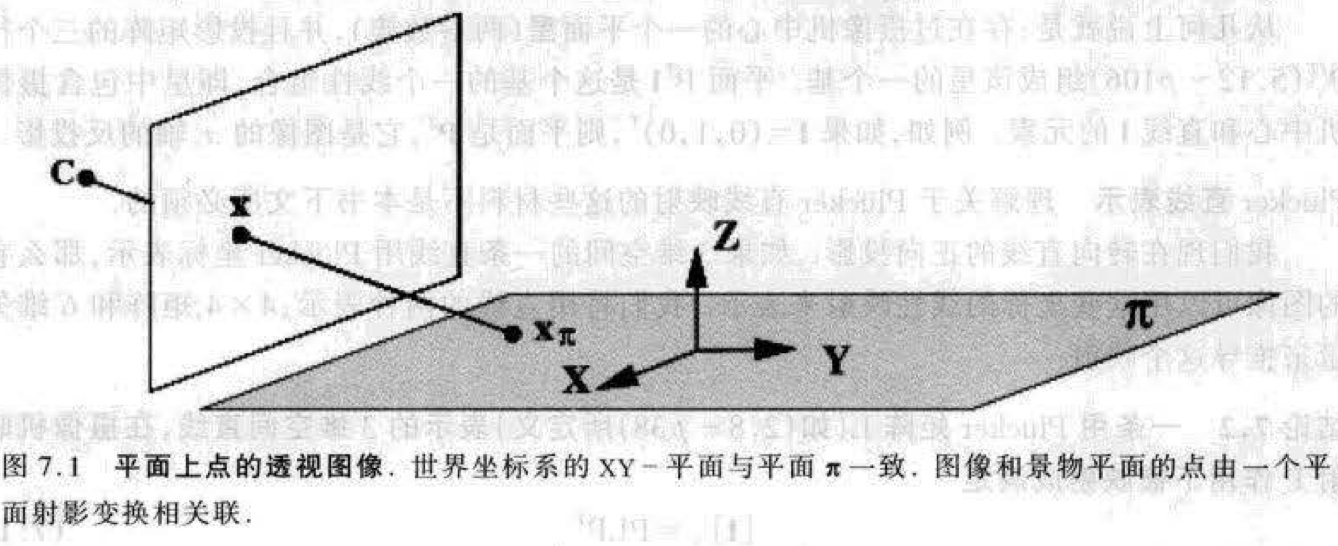
假定选择 XY - 平面与景物中的平面\(\pi\)对应，使得平面上的点\(Z\)坐标为零。
- \(\mathbf{x}=P\mathbf{X}=[\mathbf{p}_1 \ \mathbf{p}_2 \ \mathbf{p}_3 \ \mathbf{p}_4] \begin{bmatrix} X \\ Y \\ 0 \\ 1 \end{bmatrix}=[\mathbf{p}_1 \ \mathbf{p}_2 \mathbf{p}_4]\begin{bmatrix} X \\ Y \\ 1 \end{bmatrix}\)
- 即\(\mathbf{x}=H\mathbf{x}_\pi\)。在透视影像下，一张景物平面与一张图像平面之间最一般的变换是平面射影变换

对直线的作用¶

正向投影：\(\mathbf{A}\)和\(\mathbf{B}\)是 3 维空间的点，而\(\mathbf{a},\mathbf{b}\)是它们在\(P\)作用下的图像：\(\mathbf{x}(\mu)=P(\mathbf{A}+\mu \mathbf{B})=P\mathbf{A}+\mu P \mathbf{B}=\mathbf{a} + \mu \mathbf{b}\)
直线的反向投影：经摄像机矩阵\(P\)映射成一条直线\(\mathbf{l}\)的空间的点集是平面\(P^\top\mathbf{l}\)
Plücker 直线表示
- 一条用 Plücker 矩阵\(L\)表示的 3 维空间直线，在摄像机映射\(P\)作用下被映射成满足\([\mathbf{l}]_\times=PLP^\top\)的直线
- 线投影矩阵\(P\)是秩为 3 的\(3 \times 6\)矩阵，即\(P=\begin{bmatrix} \mathbf{P}^2 \wedge \mathbf{P}^3 \\ \mathbf{P}^3 \wedge \mathbf{P}^1 \\ \mathbf{P}^1 \wedge \mathbf{P}^2 \end{bmatrix}\)，其中\(\mathbf{P}^{i\top}\)是点摄像机矩阵\(P\)的行，而\(\mathbf{P}^i \wedge \mathbf{P}^j\)是平面\(\mathbf{P}^i\)与\(\mathbf{P}^j\)的交线的 Plücker 坐标
- 在线投影矩阵\(P\)作用下，\(IP^3\)中用 Plücker 坐标表示的直线\(\mathcal{L}\)被映射导图像直线：\(\mathbf{l}=P\mathcal{L}=\begin{bmatrix} (\mathbf{P}^2 \wedge \mathbf{P}^3 | \mathcal{L}) \\ (\mathbf{P}^3 \wedge \mathbf{P}^1 | \mathcal{L}) \\ (\mathbf{P}^1 \wedge \mathbf{P}^2 | \mathcal{L}) \end{bmatrix}\)
- \(IP^3\)中满足\(P\mathcal{L}=\mathbf{0}\)的直线\(\mathcal{L}\)必过摄像机中心

对二次曲线的作用¶

在摄像机\(P\)作用下，二次曲线\(C\)反向投影成锥面:\(Q_{CO}=P^\top CP\)

光滑曲面的图像¶

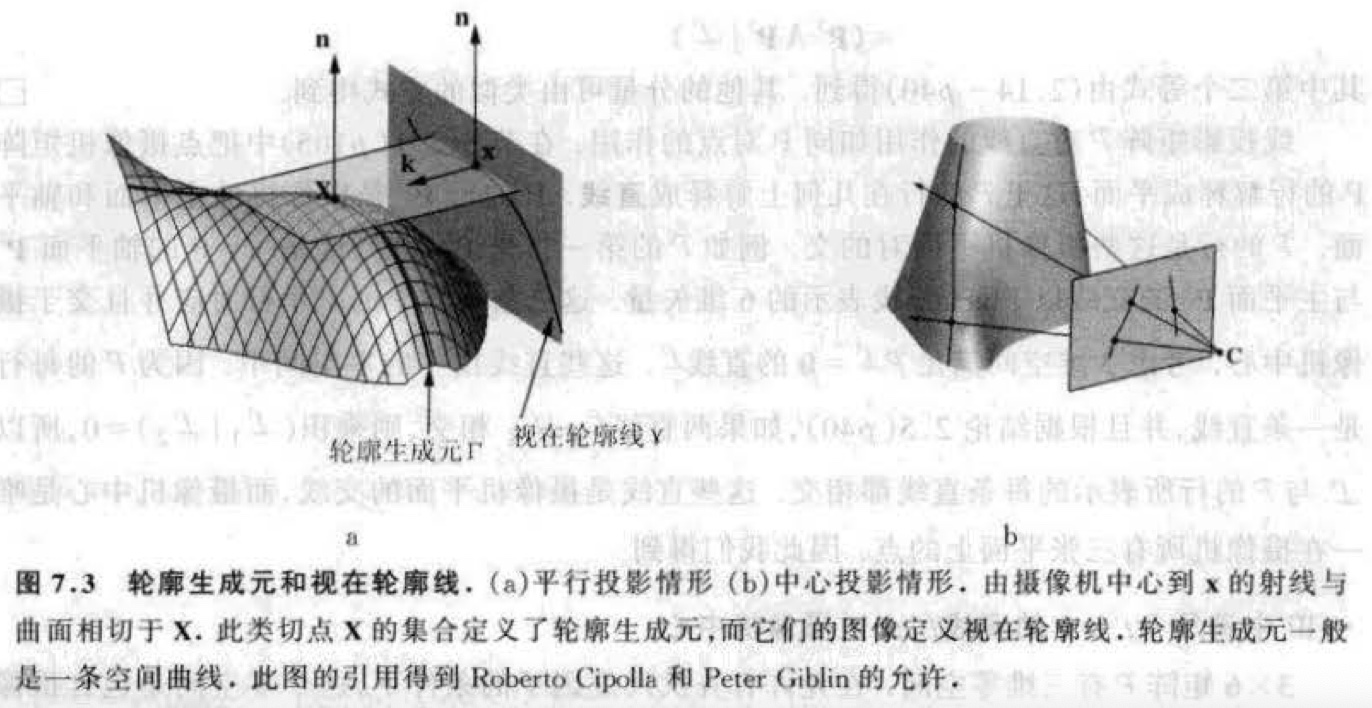
轮廓生成元\(\Gamma\)定义为影像射线与\(S\)的所有切点\(\mathbf{X}\)的集合。在图像上，与它对应的视在轮廓线\(\gamma\)是\(\mathbf{X}\)的图像点\(\mathbf{x}\)的集合，即\(\gamma\)是\(\Gamma\)的图像
- 轮廓生成元\(\Gamma\)仅取决于摄像机中心与曲面的相对位置，而与图像平面无关
- 视在轮廓线\(\gamma\)由图像平面与轮廓生成元的射线的相交确定，因此与图像平面有关

射影摄像机对二次曲面的作用¶

二次曲面的正向投影
- 在摄像机矩阵\(P\)的作用下，二次曲面\(Q\)的外形线是下式给定的一条二次曲线\(C^*=PQ^*P^\top\)
- 与二次曲面\(Q\)和中心为\(C\)的摄像机相对应的轮廓生成元\(\Gamma\)的平面是\(\pi_\Gamma=QC\)
顶点为\(\mathbf{V}\)并与二次曲面\(Q\)相切的锥面是一个退化的二次曲面\(Q_{CO}=(\mathbf{V}^\top Q\mathbf{V})Q-(Q\mathbf{V})(Q\mathbf{V})^\top\)，当\(Q_{CQ}\mathbf{V}=\mathbf{0}\)时，\(\mathbf{V}\)正是所要求的锥面的顶点

摄像机中心的重要性¶

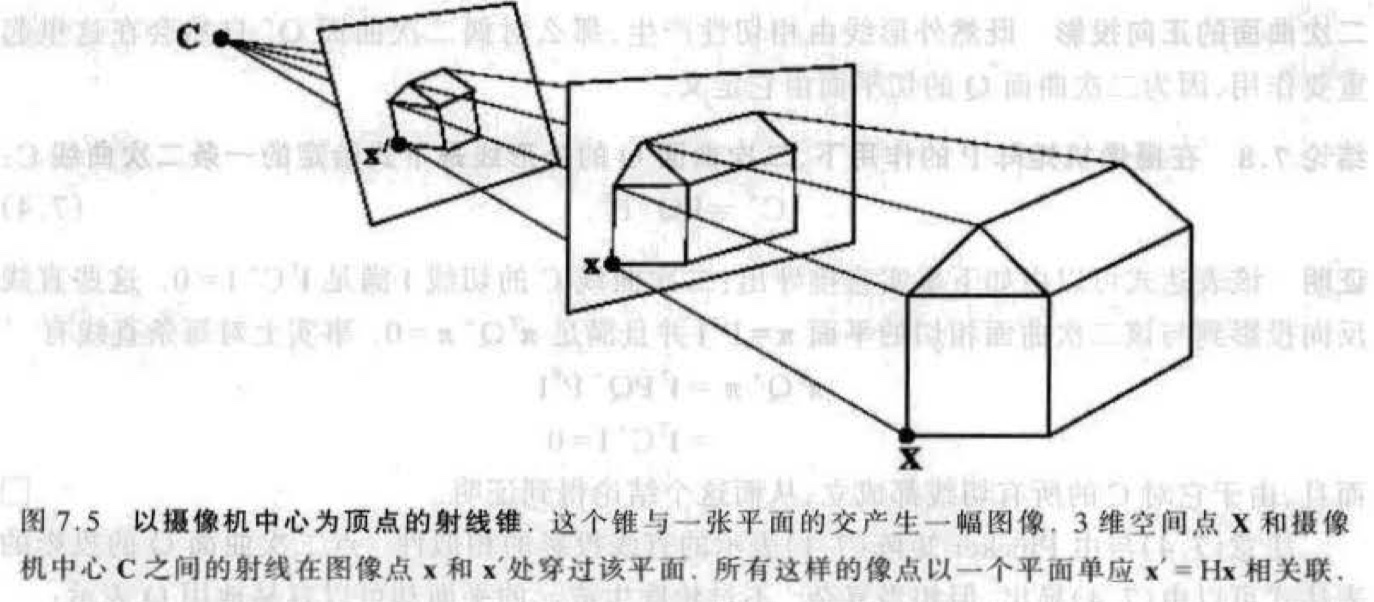
3 维空间的物体和摄像机中心确定了一个射线集合，而这些射线与一张平面的交就产生该物体的图像，这个集合通常称为射线锥
假设射线锥与两张平面相交，那么所得两幅图像\(\mathbf{I}\)和\(\mathbf{I}^\prime\)显然以一个透视映射相关联。因为摄像机有共同的中心，从而由这两个摄像机产生的 3 维空间点\(\mathbf{X}\)的图像之间的关系：\(\mathbf{x}^\prime=P^\prime \mathbf{X}=(K^\prime R^\prime)(KR)^{-1}P \mathbf{X}=(K^\prime R^\prime)(KR)^{-1} \mathbf{x}\)，对应的图像点以一个形如\(\mathbf{x}^\prime=H\mathbf{x}\)的平面单应(\(3 \times 3\)矩阵)相关联，其中\(H=(K^\prime R^\prime)(KR)^{-1}\)

移动图像平面¶

考虑焦距增加的情况，在一阶近似的精度下，它相当于图像平面沿主轴移动
因子\(k=f^\prime/f\)的变焦效果等于用\(diag(k,k,1)\)右乘摄像机标定矩阵\(K\)

摄像机旋转¶

摄像机在不改变它的内部参数的情况下绕它的中心旋转。如果点\(\mathbf{X}\)在纯旋转前和后的图像是\(\mathbf{x}\)和\(\mathbf{x}^\prime\)，那么\(\mathbf{x}^\prime=K[R|\mathbf{0}]\mathbf{X}=KRK^{-1}K[\mathbf{I}|\mathbf{0}]\mathbf{X}=KRK^{-1}\mathbf{x}\)，因此，\(\mathbf{x}^\prime=H\mathbf{x}\)，其中\(H=KRK^{-1}\)这种单应是一个共轭旋转

应用与举例¶

视图合成¶

可以对现有的图像进行平面单应性的形变插补来产生新的图像，新的图像对应于不同的摄像机定向(但摄像机中心相同)

计算把图像中的四边形映射回具有正确长宽比矩形的单应 H
用这个单应对原图像进行射影形变插补

平面全景拼图¶

摄像机绕其中心旋转所得到的一组图像之间以一个平面单应相关联。这样的一组图像可以通过射影形变插补与其中一幅图像的平面配准。

选择图像集合中的一幅作为参考图像
在其余的图像中选一幅图像，计算把它映射到参考图像的单应 H
用得到的单应对这幅图像进行射影形变插补，并且用插补图像与参考图像的非重叠部分来扩大参考图像
对图像集合中余下的图像重复上述最后两步过程

（简化的）射影记号¶

如果世界和图像点都选择规范的射影坐标那么摄像机矩阵：\(P=\begin{bmatrix} a & 0 & 0 & -d \\ 0 & b & 0 & -d \\ 0 & 0 & c & -d \end{bmatrix}\) 满足\(\mathbf{x}_i=P\mathbf{X}_i,i=1,...,4\)和\(P(a^{-1},b^{-1},c^{-1},d^{-1})^\top=\mathbf{0}\)，后者表示摄像机中心是\(\mathbf{C}=(a^{-1},b^{-1},c^{-1},d^{-1})^\top\)

移动摄像机中心¶

在第一幅视图中重合的两个 3 维空间点.郎在同一射线上的点。如果摄像机中心被移动了(没有沿着这条射线) ，那么其图像就不再重合了。原来是重合的图像点之间的相对位移称为视差。

摄像机标定与绝对二次曲线的图像¶

摄像机标定矩阵\(K\)是\(\mathbf{x}\)与在摄像机的欧氏坐标系下测量的射线方向\(\mathbf{d}=K^{-1}\mathbf{x}\)之间的一个（仿射）变换
一条图像直线\(\mathbf{l}\)确定一张过摄像机中心的平面，在摄像机的欧氏坐标系下，该平面的法线方向为\(\mathbf{n}=K^\top \mathbf{l}\)

绝对二次曲线的图像¶

\(\pi_\infty\)与图像平面之间的映射由平面单应\(\mathbf{x}=H\mathbf{d}\)给出，其中\(H=KR\)
绝对二次曲线的图像（简称 IAC）是二次曲线 \(\omega=(KK^\top)^{-1}=K^{-\top}K^{-1}\)
绝对二次曲线的对偶图像（简称 DIAC）为 \(\omega^*=\omega^{-1}=KK^\top\)

一个简单的标定装置

装置里有三个正方形（它们所在平面是不平行的，但也不必正交）的图像提供计算\(K\)的足够约束

对每个正方形，计算把它的角点\((0,0)^\top、(1,0)、(0,1)、(1,1)^\top\)映射到相应的图像点的单应\(H\)
计算该正方形所在平面虚圆点的图像，即\(H(1,\pm i,0)^\top\)
由这六个虚圆点的图像拟合出一条二次曲线\(\omega\)
用 Cholesky 分解由\(\omega=(KK^\top)^{-1}\)计算标定\(K\)

图像中的正交性
- 如果图像点关于\(\omega\)共轭，即如果\(\mathbf{x}_1^\top \omega \mathbf{x}_2 = 0\)，那么这两个图像点对应于正交的方向
- 假定直线\(\mathbf{l}\)反向投影到法线方向为\(\mathbf{n}\)的平面\(\pi\)，那么法线的影像为点\(K\mathbf{n}\)，而且直线\(\mathbf{l}\)是该点的极线，因此\(\mathbf{l}=\omega K \mathbf{n}=(KK^\top)^{-1}K\mathbf{n}=K^{-\top}\mathbf{n}\)，即\(\pi\)的法线是\(\mathbf{n}=K^\top \mathbf{l}\)

标定二次曲线¶

绝对二次曲线的图像（IAC）是图像中的一条虚二次曲线。为了可视化的目的，考虑与摄像机标定紧密相关的另外一种曲线，这样的二次曲线称为标定二次曲线，它是一个顶角为\(45^\circ\)而轴为摄像机主轴的圆锥面的图像。该圆锥面的点映射为二次曲线：

\[ C=K^{-\top} \begin{bmatrix} 1 & & \\ & 1 & \\ & & -1 \end{bmatrix} K^{-\top} \]

正交性和标定二次曲线：如果图像平面上的一条直线对应于垂直于图像点\(\mathbf{x}\)的射线的一个平面，那么，这条直线是\(\mathbf{x}\)关于标定二次曲线的反射点\(\overset{\cdot}{\mathbf{x}}\)的极线\(C\overset{\cdot}{\mathbf{x}}\)

消影点和消影线¶

透视投影的一个显著特征是延伸至无穷远的物体的图像可能出现在有限范围
消影点
- 集合上一条世界直线的消影点由平行于该直线并过摄像机中心的射线与图像平面的交点得到。因此消影点仅依赖于直线的方向，而与其位置无关。如果世界直线平行于图像平面，那么消影点在图像的无穷远处。
- 该世界直线可以用\(\mathbf{X}(\lambda)=\mathbf{A}+\lambda\mathbf{D}\)来参数化，其中\(\mathbf{A}\)是直线上的点，而\(\mathbf{D}=(\mathbf{d}^\top,0)^\top\)
- 方向为\(\mathbf{d}\)的 3 维空间直线的消影点是过摄像机中心且方向为\(\mathbf{d}\)的射线与图像平面的交点\(\mathbf{v}\)，即\(\mathbf{v}=K\mathbf{d}\)
由消影点求摄像机旋转
- 消影点是无穷远点的图像，它提供定向(姿态)信息的方式与不动星提供的方式类似，考虑由定向和位置不同的两个标定摄像机获取的一个景物的两幅图像。无穷远点作为景物的一部分与摄像机无关。它们的图像，即消影点，不受摄像机位置变化的影响，但要受摄像机旋转的影响。
- 令一条景物直线在第一幅视图中的消影点是\(\mathbf{v}_i\)，在第二幅视图中的是\(\mathbf{v}_i^\prime\)，消影点\(\mathbf{v}_i\)在第一个摄像机的欧氏坐标系中测量得到的方向是\(\mathbf{d}_i=K^{-1}\mathbf{v}_i / \parallel K^{-1} \mathbf{v}_i \parallel\)，而对应的消影点\(\mathbf{v}_i^\prime\)，在第二个摄像机的欧氏坐标系中测量得到的方向是\(\mathbf{d}_i^\prime\)，则摄像机的旋转\(\mathbf{d}_i^\prime=R\mathbf{d}_i\)
消影线
- 3 维空间的平行平面与\(\pi _\infty\)交于一条公共的直线，而这条直线的图像就是平面的消影线。几何上，消影线由平行于景物平面并过摄像机中心的一张平面与图像的交线得到。显然，消影线仅与景物平面的定向有关，而与它的位置无关。
- 在摄像机欧氏坐标系下，垂直于方向\(\mathbf{n}\)的平面集的消影线是\(\mathbf{l}=K^{-\top}\mathbf{n}\)
两条景物直线之间的夹角：令\(\mathbf{v}_1,\mathbf{v}_2\)是一幅图像中两条直线的消影点，而令\(\omega\)为图像中绝对二次曲线的图像。如果\(\theta\)是两直线方向间的夹角，则

\[ \cos \theta = \frac{\mathbf{v}_1^\top \omega \mathbf{v}_2}{\sqrt{\mathbf{v}_1^\top \omega \mathbf{v}_1} \sqrt{\mathbf{v}_2^\top \omega \mathbf{v}_2}} \]

正交性关系
- 具有垂直方向的直线的消影点满足\(\mathbf{v}_1^\top \omega \mathbf{v}_2=0\)
- 一张平面的法线方向的消影点\(\mathbf{v}\)可以按公式\(\mathbf{v}=\omega^*\mathbf{l}\)由平面的消影线\(\mathbf{l}\)获得；反之有\(\mathbf{l}=\omega \mathbf{v}\)
- 两垂直平面的消影点满足\(\mathbf{l}_1^\top \omega^* \mathbf{l}_2=0\)

由消影点和消影线确定标定 K¶

如果\(s=K_{12}=0\)，并且\([\omega_{ij}]=\omega=K^{-\top}K^{-1}\)，那么\(\omega_{12}=\omega_{21}=0\)，如果还满足\(\alpha_x=K_{11}=K_{22}=\alpha_y\)，那么\(\omega_{11}=\omega_{22}\)

由三个正交消影点给定的标定二次曲线

首先构作顶点为三个消影点\(\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\)的三角形
\(C\)的中心是三角形的垂心
关于中心反射其中的一个消影点（例如\(\mathbf{v}_1\)）得到\(\overset{\cdot}{\mathbf{v}}_1\)
根据条件：\(\overset{\cdot}{\mathbf{v}}_1\)的极线过\(\mathbf{v}_2, \mathbf{v}_3\)来确定\(C\)的半径