2D 射影几何和变换¶
约 4639 个字 7 张图片 预计阅读时间 15 分钟
Abstract
本章主要介绍MVG所必须的几何概念和符号,具体涵盖平面的射影变换几何
平面几何¶
2D 射影平面¶
点与直线¶
-
直线的其次表示
平面上的一条直线的方程\(ax+by+c=0\)可以用矢量\((a,b,c)^{\top}\)表示。对任何非零的k矢量\((a,b,c)^{\top}\)与\(k(a,b,c)^{\top}\)表示同一直线。
-
点的其次表示
一个点的任何齐次矢量的表示形式为\(x=(x_1,x_2,x_3)^{\top}\),非齐次坐标\(x=(\frac{x_1}{x_3}, \frac{x_2}{x_3})^{\top}\)。
-
结论1
点\(x\)在直线\(l\)的充要条件是\(x^{\top}l=0\)。\(x^{\top}l = l^{\top}x = x \cdot l = 0\)。
-
结论2
两直线\(l\)和\(l^{\prime}\)的交点是点\(x=l \times l^{\prime}\)。
叉乘
-
结论3
过两点\(x\)和\(x^{\prime}\)的直线是\(l = x \times x^{\prime}\)。
-
平行线的交点
两平行直线\(ax+by+c=0\)和\(ax+by+c^{\prime}=0\),由结论2可得交点\((b, -a, 0)^{\top}\)。
-
理想点和无穷远线
当齐次矢量\(x = (x_1, x_2, x_3)^{\top}\)中的\(x_3=0\)时的点被称为理想点,或无穷远点。所有理想点集合在一条直线上,称无穷远线,用\(I_{\infty}=(0,0,1)^{\top}\)表示。
-
射影平面模型
\(IP^2\)的点和线分别为中过原点的射线和平面\(x_1x_2\)平面上的射线表示理想点,而\(x_1x_2\)平面表示\(I_{\infty}\)。
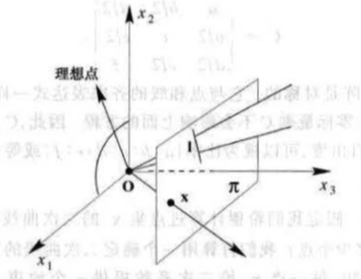
-
结论4(对偶原理)
2维射影几何中的任何定理都有一个对应的对偶定理,它可以通过互换原定理中点和线的作用而导出。
二次曲线与对偶二次曲线¶
-
二次曲线
在欧氏几何中,二次曲线有三种主要类型: 双曲线,椭圆和抛物线。
在非齐次坐标中,二次曲线的方程是
\[ax^2+bxy+cy^2+dx+ey+f=0\]通过替代\(x\to\frac{x_1}{x_3}\),\(y\to\frac{x_2}{x_3}\),得到:
\[ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0\]表示成矩阵形式为\(x^{\top}Cx=0\) 其中二次曲线系数矩阵\(C\)为
\[ C = \left[ \begin{matrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{matrix} \right] \] -
结论5
过(非退化)二次曲线\(C\)上点\(x\)的切线\(l\)由\(l=Cx\)确定。
-
对偶二次曲线
上面定义的二次曲线\(C\)更确切地应称为点二次曲线,因为它定义的是点的方程。同时这种对偶(或线)二次曲线也由一个\(3 \times 3\)矩阵表示,我们把它记为\(C^*\),二次曲线\(C\)的切线\(l\)满足\(l^{\top}C^*l=0\)。其中\(C^*\)表示为\(C\)的伴随矩阵。
-
退化二次曲线
非满秩矩阵\(C\)所定义的二次曲线称作退化二次曲线。退化的点二次曲线包含两条线(秩 2) 或一条重线(秩 1) 。
射影变换¶
-
射影映射
射影映射是\(IP^2\)到它自身的一种满足下列条件的可逆映射\(h\):三点\(x_1\),\(x_2\)和\(x_3\)共线当且仅当\(h(x_1)\),\(h(x_2)\),\(h(x_3)\)也共线。射影映射也称为保线变换 ,或射影变换或单应 (homography)。
-
定理1
映射\(h\):\(IP^2 \to IP^2\)是射影映射的充要条件是存在一个\(3 \times 3\)非奇异矩阵\(H\),使得\(IP^2\)的任何一个用矢量\(x\)表示的点都满足\(h(x)=Hx\)。
-
射影变换
平面射影变换是关于齐次3维矢量的一种线性变换,并可用一个非奇异\(3 \times 3\)矩阵\(H\)表示为:
\[ \begin{pmatrix} x_1^\prime \\ x_2^\prime\\ x_3^\prime \end{pmatrix} = \left[ \begin{matrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{matrix} \right] \begin{pmatrix} x_1 \\ x_2\\ x_3 \end{pmatrix} \]或更简洁地表示为\(x^\prime = Hx\)。
直线和二次曲线的变换¶
-
直线的变换
\[l^\prime = H^{-T}l\]也可以写成\(l^{\prime T}=l^{\top}H^{-1}\)。直线和点变换的基本区别在于点变换依据\(H\),而直线(视为行矢量)变换则依据\(H^{-1}\)。称点变换为逆变而线变换为协变。
-
二次曲线的变换
在点变换\(x^\prime = Hx\)下,\(x^{\top}Cx = x^{\prime T}[H^{-1}]^{\top}CH^{-1}x^\prime = x^{\prime T} H^{-T}CH^{-1} x^{\prime}\)。
-
结论1
在点变换\(x^\prime = Hx\)下,二次曲线\(C\)变换为\(C^\prime = H^{-T}CH^{-1}\)。(因为存在\(H^{-1}\),所以称二次曲线变换为协变)
证明
\[ x^{\top}Cx = (H^{-1}x^\prime)^{\top} C (H^{-1}x^\prime) = x^{\prime T} (H^{-T}CH^{-1}) x^\prime \] -
结论2
在点变换\(x^\prime = Hx\)下,对偶二次曲线\(C^*\)变换为\(C^{*\prime} = HC^* H^{\top}\)。
证明
\[ l^{\top}C^*l = (H^{\top}l)^{\top}C^*(H^{\top}l)=l^{\top}HC^*H^{\top}l \]
-
变换的层次¶
由\(n \times n\)可逆实矩阵的群称为(实的)一般线性群或\(GL(n)\)。当, 把相差非零纯靠因子的矩阵都视为等同时,便得到射影线性群,记为\(PL(n)\)(它是\(GL(n)\)的商群)。在平面射影变换时,\(n=3\)。
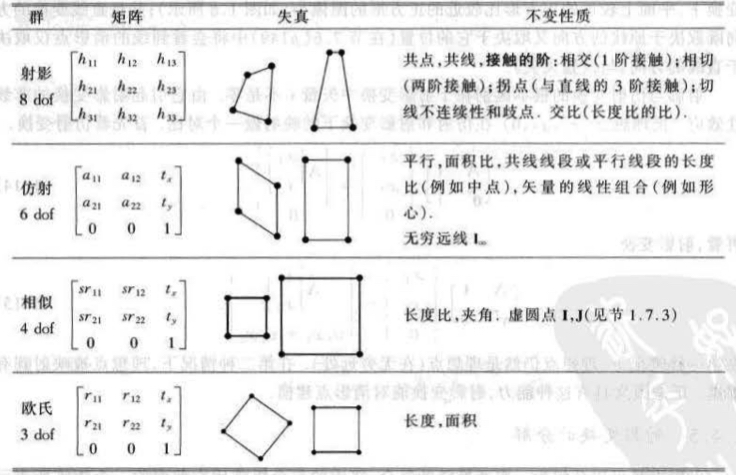
等距变换¶
等距(isometric)变换是平面\(IR^2\)的变换,保持欧式距离不变,一个等距变换可表示为
其中\(\varepsilon = \pm 1\)。如果\(\varepsilon = 1\)那么该等距变换是保向的并且也是欧氏变换(平移和旋转的复合)。如果\(\varepsilon = -1\),那么该等距变换是逆向的。
平面欧氏变换可以用更简洁的分块形式写为
平面欧氏变换有三个自由度,旋转一个,平移二个。
- 不变量:长度(两点的距离),角度(两线的夹角)和面职。
- 群和定向 保向的等距变换形成一个群,但逆向的不是。这种区别对于下面的相似和仿射变换同样如此。
相似变换¶
相似变换是一个等距变换与一个均匀缩放的复合。矩阵表示为:
可以用更简洁的分块形式写为
- 不变量:直线的夹角,两长度的比率和面积的比率。
仿射变换¶
仿射变换是一个非奇异线性变换与一个平移变换的复合,它的矩阵表示为:
可以用更简洁的分块形式写为
平面仿射变换有六自由度,可以由三组点对应来计算。
- 不变量:平行线,平行线段的长度比和面积比。
射影变换¶
它是齐次坐标的一般非奇异线性变换,其分块形式:
其中\(\mathbf{v}=(v_1, v_2)^{\top}\)。
射影变换由八个参数确定,可由四组点对应算出, 但其中属于向一平面的三点必不共线。
- 不变量:最基本的射影不变量是四共线点的交比。
射影变换的分解¶
射影变换可以分解为一串变换链的复合,链中的每个矩阵比它前面的一个矩阵所表示的变换层次高。
其中\(A=sRK+\mathbf{tv}^{\top}/v\),而\(K\)是满足\(det\ K=1\)的归一化上三角矩阵。如果\(v \ne 0\)上述分解是有效的,而且如果\(s\)取正值,它还是唯一的。
- 不变量的数目:与函数无关的不变量数等于或大于配置的自由度数减去变换的自由度数。
1D 射影几何和交比¶
直线上的点\(x\)用齐次坐标表示为\((x_1, x_2)^{\top}\),而\((x_1, 0)^{\top}\)是该直线的理想点。我们将用记号\(\mathbf{\bar{x}}\)表示\(2\)维矢量\((x_1, x_2)^{\top}\)。可用齐次矩阵表示:
\[\mathbf{\bar{x}}^\prime = H_{2 \times 2} \mathbf{\bar{x}}\]
交比¶
交比是\(IP^1\)的基本射影不变量。给定\(4\)个点\(\mathbf{\bar{x}_i}\),交比定义为
其中
-
交比的主要特点
- 交比的值与各点\(\mathbf{\bar{x}_i}\)所用的具体的齐次表示无关。
- 如果每点\(\mathbf{\bar{x}_i}\)都是有限点,并且在齐次表示中均选择\(x_2 = 1\),那么\(|\mathbf{\bar{x}_i}\mathbf{\bar{x}_j}|\)就表示由\(\mathbf{\bar{x}_i}\)到\(\mathbf{\bar{x}_j}\)的带符号的距离。
- 如果点\(\mathbf{\bar{x}_i}\)中有一个理想点,交比的定义仍然有效。
- 在任何直线的射影变换下,交比的值不变。
-
共点线
共点线是直线上共线点的对偶。这意味着平面上的共点线也有几何\(IP^1\)。特别是,任何四条共点线都有一个确定的交比。
从图像恢复仿射和度量性质¶
射影矫正的目的是消除平面的透视图像中的射影失真,使得原始平面的相似性质(角度、长度比)可以被测量。
无穷远线¶
在射影变换下,理想点可以映射为有限点,因而\(I_{\infty}\)被映射为有限直线。但如果是仿射变换,\(I_{\infty}\)不会被映射为有限直线,即仍留在无穷远处,显然,它可直接由直线的变换推出:
-
结论1
在射影变换\(H\)下,无穷远直线\(I_{\infty}\)为不动直线的充要条件是\(H\)是仿射变换。
在平面的像中,一但无穷远直线的像得到辨认,就有可能对原平面进行仿射测量。如下图所示,直接把已辨认的\(I_\infty\)变换到它的规范位置\(I_\infty = (0,0,1)^{\top}\)。把实现此变换的(射影)矩阵应用于图像中的每一点以达到对图像进行仿射矫正的目的,即变换之后,仿射测量可以直接在矫正过的图像中进行。
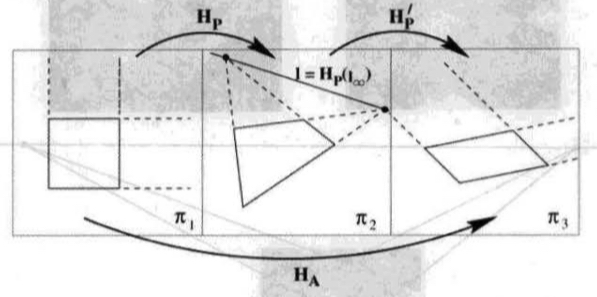
如果无穷远直线的像是\(\mathbf{I} = (l_1, l_2, l_3)^{\top}\),假定\(l_3 \ne 0\),那么把\(\mathbf{l}\)映射回\(l_\infty = (0,0,1)^{\top}\)的一个合适的射影点交换是
-
直线上的距离比
给定一个直线上有已知长度比的两个线段,该直线上的无穷远点便可以确定。
虚圆点及其对偶¶
-
虚圆点
每一圆周与\(l_\infty\)相交的点称为虚圆点。
证明
在二次曲线为圆有\(a=c\)且\(b=0\)。取\(a=1\)则:
\[x_1^2+x_2^2+dx_1x_3+ex_2x_3=fx_3^2=0\]该二次曲线相交于\(l_\infty\)于(理想)点(\(x_3=0\)):
\[x_1^2+x_2^2=0\]解得虚圆点的标准坐标是\(\mathbf{I}=(1,i,0)^{\top}, \; \mathbf{J}=(1, -i, 0)^{\top}\)。
这一对虚圆点是复共轭理想点,它们在保向相似变换下不变:
\[ \mathbf{I}^\prime = H_S\mathbf{I} = \left[ \begin{matrix} s\cos \theta & -s\sin \theta & t_x \\ s\sin \theta & s\cos \theta & t_y \\ 0& 0 & 1 \end{matrix} \right] \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} = se^{-i \theta} \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix} = \mathbf{I} \] -
结论2
在射影变换\(H\)下,虚圆点\(I\)和\(J\)为不动点的充要条件是\(H\)是相似变换。
任何圆都交\(\mathbf{I}_\infty\)于虚圆点 . 在欧氏几何中一个圆由三点指定.虚圆点引出另 一种计算.圆可以用由五个点定义的一般二次曲线的公式(三个点加两个虚圆点)。虚圆点是把欧氏几何中的两正交方向合并到一个复共轭中,即
\[\mathbf{I}=(1,0,0)^{\top} + i(0,1,0)^{\top}\] -
与虚圆点对偶的二次曲线
\[C_{\infty}^* = \mathbf{I}\mathbf{J}^{\top}+\mathbf{J}\mathbf{I}^{\top}\] -
结论3
对偶二次曲线\(C_{\infty}^*\)在射影变换\(H\)下不变的充要条件是\(H\)相似变换。
此外,在任何射影框架下,\(C_{\infty}^*\)具有一些性质:
- \(C_{\infty}^*\)有\(4\)个自由度
- \(\mathbf{I}_\infty\)是\(C_{\infty}^*\)的零矢量
射影平面上的夹角¶
在欧氏几何中,两线间的夹角由它们法线的点乘来计算。直线\(\mathbf{I}=(l_1, l_2, l_3)^{\top}\)和\(\mathbf{m}=(m_1, m_2, m_3)^{\top}\)的法线分别平行于\((l_1, l_2)^{\top}\)\((m_1, m_2)^{\top}\),其夹角为
\[\cos \theta = \frac{l_1m_1+l_2m_2}{\sqrt{(l_1^2+l_2^2)(m_1^2+m_2^2)}}\]在射影变换下不变的公式为:
\[\cos \theta = \frac{\mathbf{I}^{\top}C_{\infty}^*\mathbf{m}}{\sqrt{(\mathbf{I}^{\top}C_{\infty}^*\mathbf{I})(\mathbf{m}^{\top}C_{\infty}^*\mathbf{m})}}\]其中\(C_\infty^*\)是与虚圆点对偶的二次曲线。
-
结论4
一旦二次曲线\(C_\infty^*\)在射影平面上被辨认,那么欧氏角可以测量。
-
结论5
如果\(\mathbf{I}^{\top}C_{\infty}^*\mathbf{m}=\mathbf{0}\),则直线\(l\)和\(m\)正交。
-
结论6
一旦二次曲线\(C_\infty^*\)在射影平面上被辨认,长度比同样可以测量。
由图像恢复度量性质¶
把虚圆点变换到它们的标准位置,就可以由平面的图像恢复度量性质。对偶二次曲线\(C_\infty^*\)几乎包含了实现度量矫正所需的全部信息。它能确定射影变换中的仿射和射影成分,而只留下相似变换的失真。
-
结论7
在射影平面上,一旦\(C_\infty^*\)被辨认,那么射影失真可以矫正到相差一个相似变换。
二次曲线的其他性质¶
极点-极线关系¶
点\(\mathbf{x}\)和二次曲线\(C\)定义一条直线\(\mathbf{l}=C\mathbf{x}\),\(\mathbf{l}\)称为\(\mathbf{x}\)关于\(C\)的极线,而点\(\mathbf{x}\)称为\(\mathbf{l}\)关于\(C\)的极点。
- 点\(\mathbf{x}\)关于二次曲线\(C\)的极线\(\mathbf{l}=C\mathbf{x}\)交于两点。\(C\)的过这两点的两条切线相交于\(\mathbf{x}\)。
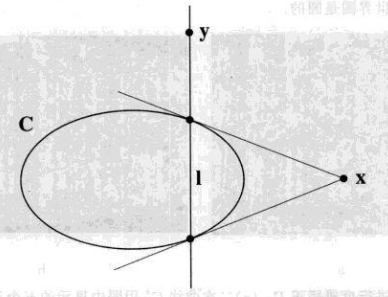
-
如果点\(x\)在\(C\)上,则它的极线就是二次曲线过\(x\)点的切线。
-
对射
- 定义:对射是\(IP^2\)点到\(IP^2\)线的可逆映射。并用一个\(3 \times 3\)非奇异矩阵\(A\)表示为\(\mathbf{l}=A\mathbf{x}\)。
- 共轭点:如果点\(y\)在极线\(\mathbf{l}=C\mathbf{x}\)上,则\(\mathbf{y}^{\top}\mathbf{l}=\mathbf{y}^{\top}C\mathbf{x}=0\)。满足\(\mathbf{y}^{\top}C\mathbf{x}=0\)的任何两点\(x,y\)称为关于二次曲线\(C\)共轭。
- 如果\(\mathbf{x}\)在\(\mathbf{y}\)的极线上,那么\(\mathbf{y}\)也在\(\mathbf{x}\)的极线上。
二次曲线的分类¶
二次曲线的射影标准形式¶
任何二次曲线都射影等价于一个由对角矩阵表示的二次曲线。二次曲线\(D\)最终被表示为具有矩阵\(diag(\varepsilon_1, \varepsilon_2, \varepsilon_3)\)的二次曲线,其中\(\varepsilon_i=\pm 1\)或\(0\)。
| 对角线 | 方程 | 二次曲线类型 |
|---|---|---|
| \((1,1,1)\) | \(x^2+y^2+w^2=0\) | 假二次曲线--无实点 |
| \((1,1,-1)\) | \(x^2+y^2-w^2=0\) | 圆 |
| \((1,1,0)\) | \(x^2+y^2=0\) | 单个实点\((0,0,1)^{\top}\) |
| \((1,-1,0)\) | \(x^2-y^2=0\) | 两条直线\(x=\pm y\) |
| \((1,0,0)\) | \(x^2=0\) | 单条直线\(x=0\)计两次 |
二次曲线的仿射分类¶
在欧氏几何中,(非退化或真)二次曲线可以分为双曲线、椭圆和抛物线。在射影几何中三种类型的二次曲线与\(l_\infty\)的关系如下图所示:
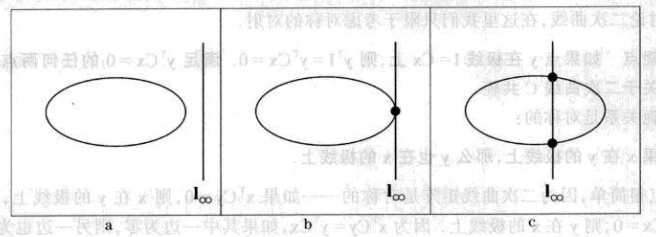
上图中二次曲线是\((a)\)椭圆,\((b)\)抛物线,\((c)\)双曲线。它们与\(l_{\infty}\)的关系 :\((a)\)无实交点、\((b)\)相切(\(2\)点接触)、\((c)\)有\(2\)个实交点。
不动点与直线¶
变换的一个特征矢量对应一个不动点,因为对于特征值\(\lambda\)及其对应的特征矢量\(e\)有:
\[H\mathbf{e} = \lambda \mathbf{e}\]而\(\mathbf{e}\)和\(\lambda \mathbf{e}\)表示同一点。类似的推导可以用于不动直线,它对应于\(H^{\top}\)的特征矢量。
平面射影变换的不动点与直线
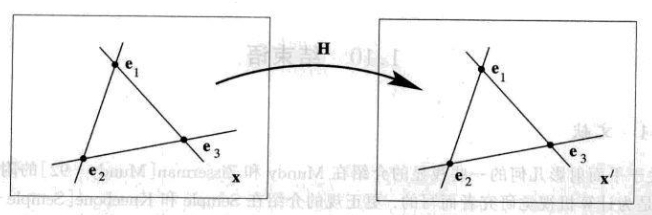
这里有三个不动点和过这三点的不动直线.不动直线和不动点可能是复的:从代数的角度来说,不动点是点变换\((\mathbf{x}^\prime=H\mathbf{x})\)的特征矢量\(\mathbf{e}_i\),而不动直线是线变换\((\mathbf{l}^\prime =H^{-T}\mathbf{l})\)的特征矢量。注意,不动直线不是点点不动:在变换下,直线上的一点被映为其上的另一点,只有不动点才映为自身。
欧氏矩阵¶
两个不动理想点是虚圆点\(\mathbf{I},\mathbf{J}\)组成的复共轭对,相对应的特征值是\(|e^{i \theta}, e^{-i \theta}|\),这里\(\theta\)是旋转角。对应于特征值\(1\)的第三个特征向量,称为\(极点\)。欧氏变换等价于绕该点转\(\theta\)角的纯旋转并且没有平移。一种特殊的情识是纯平移(即\(\theta=0\))。这时特征值三重退化,这是约束透视变换的一个例子。
相似矩阵¶
两个不动理想点仍是虚圆点。特征值是\(|1,se^{i \theta}, se^{-i \theta}|\)。相似变换的作用可以理解为绕它的有限不动点的旋转和取\(s\)为因子的均匀缩放。注意虚圆点的特征值仍然表征旋转角。
仿射矩阵¶
两个不动理想点可以是实或复共轭的,但在任何一种情况下,过这些点的不动直线\(\mathbf{l}_\infty=(0,0,1)^{\top}\)是实的。