4DGaussians¶

Idea¶

Introduction¶

• 3DGS 只能在静态场景重建，如果发生运动，则需要考虑时间维度的信息，把 3DGS 的思想放到对动态空间的建模上
• 最简单的想法就是在每一个时间点上单独建立一个 3DGS 模型，将一段时间上所有的 3DGS 模型组合起来就是一个 4DGS 模型，但这样会代码存储空间爆炸的问题
• 4DGS 的创新点在于，在 3DGS 的基础上，引入变形场 (deformation field) 来表示 Gaussians 的运动和形变，包括一个多分辨率特征平面和一个轻量级 MLP，简单地说，将动态场景看作是一个静态场景在时间维度上的变形
• 在每个时间戳，变形场会将 Gaussians 转换到一个具体新形状的新位置，该变换相当于 Gaussian 的运动和形变（从始至终只维护一组 3DGS 模型，即只有一组 3D 高斯球，只是在不同的时间节点，高斯球会做出相应的变换）
• 4DGS 模型中，将一个点的 $(x,y,z,t)$ 坐标先代入一个时空结构编码器，随后输出带入一个多头的高斯变形解码器进行解码，得到 $(x,y,z,r,s)$ 的变形值，与原值相加后，按照 3DGS 的方法得到不透明度和 SH 系数进行渲染

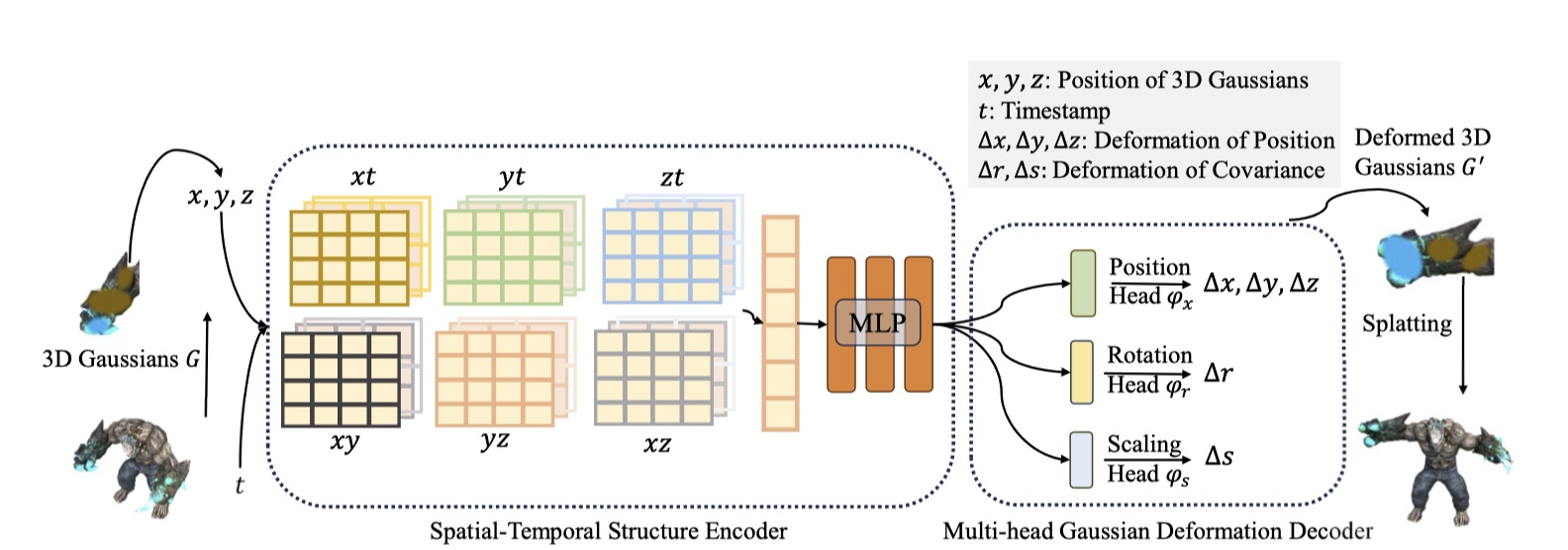
4D Gaussian Splatting Framework¶

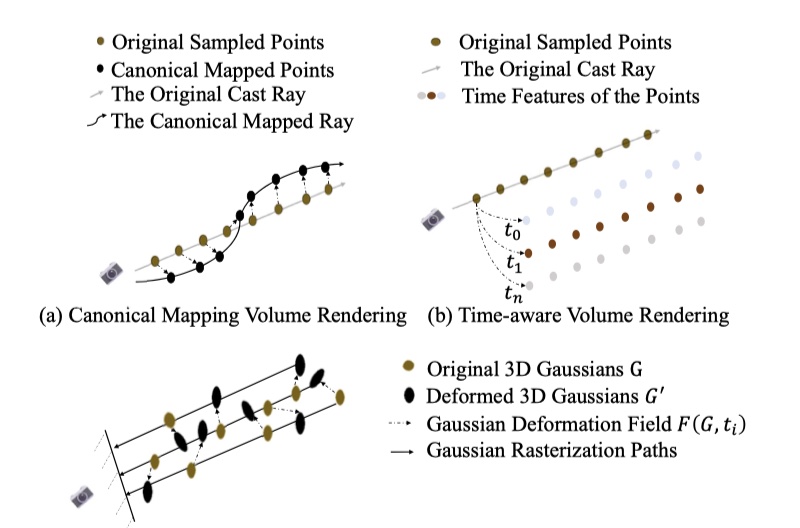
Gaussian Deformation Field Network¶

Spatial-Temporal Structure Encoder¶

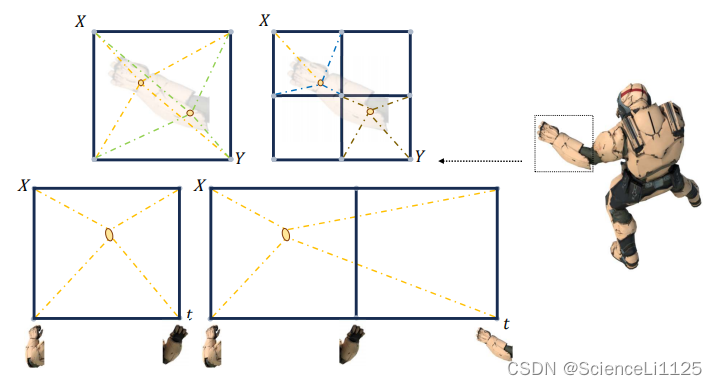
• 如上图所示，空间相邻的高斯在运动和形变上具有相似的特征，同一个高斯在相邻时间也会呈现相似的变化特征，并且相隔较远的高斯之间也会具有一定的关联。
  • 因此 4DGS 采用多分辨率特征平面体素网格模块对单元体素中的每个高斯的空间和时间进行编码
• $\mathcal{H}$ 包括六个多分辨率平面模块 $R_l(i,j)$ 和一个小型 MLP $\phi_d$
  • $\{R_l(i,j), \phi_d | (i,j) \in \{ (x,y),(x,z),(y,z),(x,t),(y,t),(z,t)\}, l \in \{1, 2 \} \}$，$\mu = (x,y,z)$ 是 3D 高斯的平均值
• 计算体素特征：

• $f_h$ 是神经体素特征，利用双线性插值对附近的四个查询体素特征进行插值
• 随后用 MLP 将所有原始特征进行解码 $f_d = \phi_d(f_h)$

Multi-Head Gaussian Deformation Decoder¶

• 设计多头高斯变形解码器 $\mathcal{D} = \{ \phi_x, \phi_r, \phi_s \}$
• 用 MLP 分别预测变形量
  • 高斯球位移变化量 $\Delta \mathcal{X} = \phi_x(f_d)$
  • 高斯球旋转四元数变化量 $\Delta r = \phi_r(f_d)$
  • 高斯球缩放因子变化量 $\Delta s = \phi_s(f_d)$
• 变形后的特征表示为 $(\mathcal{X}^\prime, r^\prime, s^\prime) = (\mathcal{X} + \Delta \mathcal{X}, r + \Delta r, s + \Delta s)$
• 最后获得出高斯球动态变化后的新形状新位置 $\mathcal{G}^\prime = \{ \mathcal{X}^\prime, s^\prime, r^\prime, \sigma, \mathcal{C} \}$

Optimization¶

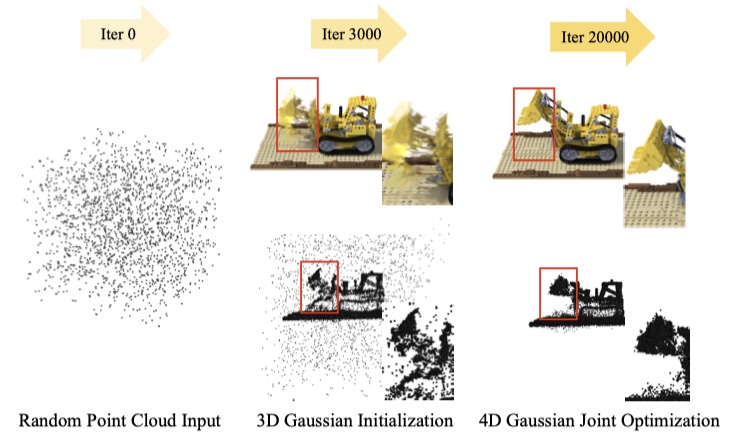
3D Gaussian Initialization¶

• 采取了两阶段训练策略：静态场景初始化和变形场微调；
  • 初始化阶段：主要优化静态场景的表示，即只优化 3D Gaussians 的参数；
  • 微调阶段：主要学习变形场的表示，即优化多分辨率神经体素和 MLP；

Loss Function¶

• 使用 $L_1$ 颜色损失和基于网格的 TV 损失 $\mathcal{L}_{tv}$ 监督训练

Experiments¶

Reference¶

• https://blog.csdn.net/m0_51976564/article/details/134595401
• https://zhuanlan.zhihu.com/p/663337795
• https://blog.csdn.net/weixin_71780622/article/details/136063893
• https://blog.csdn.net/m0_55605361/article/details/141122450