FreeTimeGS¶
约 1059 个字 1 张图片 预计阅读时间 4 分钟
Abstract
Introduction¶
问题导向
现有方法通常在规范空间中定义 3D Gaussian,并使用变形场将规范空间映射到观测空间,然而这些方法难以处理复杂的运动场景,原因在于变形场的优化难度较大。
解决方案
Method¶
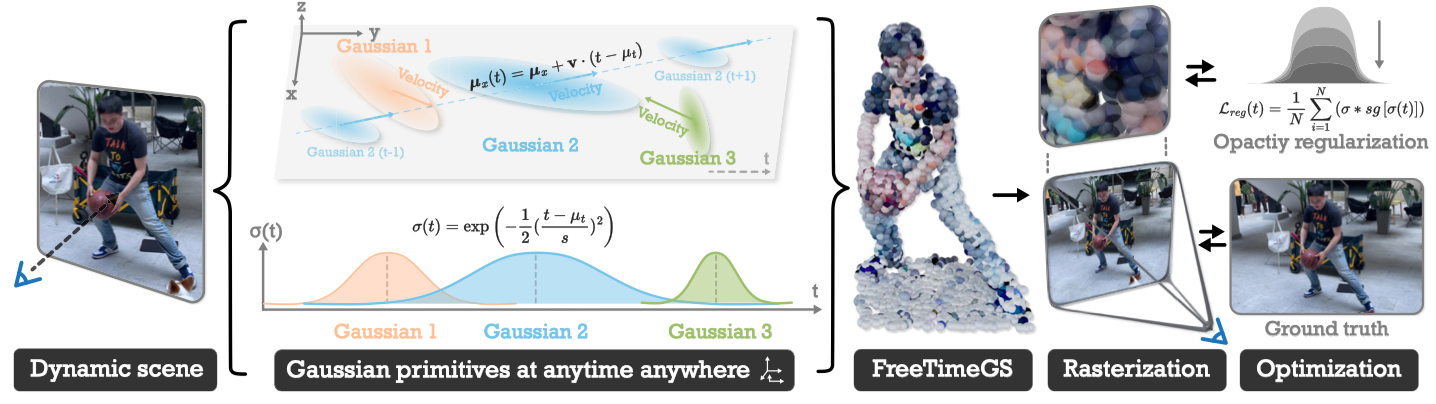
Gaussian primitives at anytime anywhere¶
- 为表示动态 3D 场景,定义了可出现在任何空间位置和时间步的 Gaussian Primitives;
- 为每个 Gaussian 分配一个运动函数,允许其随时间动态调整自身位置至邻近区域,增强几何结构和外观;
- 每个 Gaussian 包含 8 个可学习参数:位置、时间、持续时间、速度、尺度、方向、不透明度和球谐函数;
- 计算 Gaussian 在任意 \((x,t)\) 处的不透明度和颜色,首先根据运动函数移动该高斯基元,以获得其在时间 \(t\) 的实际空间位置 \(\boldsymbol{\mu}_x(t)=\boldsymbol{\mu}_x+\mathbf{v}\cdot(t-\mu_t)\);
- 基于 moved-Gaussian,通过球谐函数得到位置 \(x\) 处的颜色:\(\mathbf{c}=\sum_{l=0}^L\sum_{m=-l}^l\mathbf{c}_{lm}Y_{lm}(\mathbf{d}(\boldsymbol{\mu}_x(t)))\);
- 在位置 \(x\) 和时间 \(t\) 处的不透明度为:\(\sigma(\mathbf{x},t)=\sigma(t)*\sigma*\exp\left(-\frac{1}{2}\left(\mathbf{x}-\boldsymbol{\mu}_{x}(t)\right)^T\boldsymbol{\Sigma}^{-1}\left(\mathbf{x}-\boldsymbol{\mu}_{x}(t)\right)\right)\);
- 为了使 Gaussian 的时间和持续时间能够通过渲染梯度自动调整,时间不透明度是一个带有缩放参数的单峰函数,因此将 \(\sigma(t)\) 建模为 Gaussian distribution:\(\sigma(t) = \exp \left( -\frac{1}{2} (\frac{t-\mu_t}{s})^2 \right)\);
为什么运动函数是线性函数,岂不是不可以模拟曲线运动?
一条曲线可以是 \(N\) 个段组成,每个段可以通过线性来移动,整体上进而模拟曲线运动。
Training¶
- 与 3DGS 类似,最小化渲染损失来优化参数:\(\mathcal{L}_{render} = \lambda_{img} \mathcal{img} + \lambda_{ssim} \mathcal{L}_{ssim} + \lambda_{perc} \mathcal{L}_{perc}\);
仅通过渲染损失来优化,会导致在快速移动或复杂运动区域的渲染质量不佳。
分析 Gaussian 的不透明度分布,发现其中很大一部分接近 1,因此总结原因是,一些 Gaussian 的高不透明度会阻止梯度反向传播到所有 Gaussian,从而阻碍优化过程。
4D Regularization¶
- 设计一种正则化损失来约束 Gaussian 的高不透明度值:
\[
\mathcal{L}_{reg}(t) = \frac{1}{N} \sum_{i=1}^{N} (\sigma * sg[\sigma(t)])
\]
Periodic relocation of primitives¶
尽管正则化损失能有效提升渲染质量,但会导致表示同一场景所需的 Gaussian 数量急剧增加。
- 设计一种周期性重定位策略,将低不透明度的 Gaussian 移动到高不透明度区域,为每个 Gaussian 设计一个采样分数 \(s\),用于衡量需要更多 Gaussian 的区域,每经过 \(N\) 次迭代,将不透明度低于阈值的 Gaussian 移动到采样分数高的区域:
\[
s=\lambda_g\triangledown_g+\lambda_o\sigma
\]
Initialization of representation¶
- 对于每个视频帧,首先使用 ROMA 来获取多视图图像间的二维匹配,通过 3D 三角化计算三维点,这些三维点及相应的时间步长被用于初始化 Gaussian 的位置和时间;
- 通过 KNN 对两个视频帧的三维点进行匹配,并将点对之间的平移作为 Gaussian 的速度;
- 优化过程中,根据 \(\lambda_t = \lambda_0^{1-t} + \lambda_1^t\) 进行退火,\(t\) 在训练过程中从 0 变为 1,帮助模型在早期捕捉快速运动,在后期捕捉复杂运动。
 FreeTimeGS: Free Gaussian Primitives at Anytime Anywhere for Dynamic Scene Reconstruction
FreeTimeGS: Free Gaussian Primitives at Anytime Anywhere for Dynamic Scene Reconstruction