跳转至

Gaussian Splatting SLAM

约 926 个字 预计阅读时间 3 分钟

Abstract

Idea

Introduction

  • 第一个近实时 SLAM 系统，以 3DGS 作为唯一的底层场景表示，可以处理单目输入。
  • SLAM 框架内的新技术，包括用于直接相机姿态估计的李群上的解析雅可比矩阵、高斯形状的各向同性正则化和几何验证
  • 关键帧选取策略、Gaussian 的增加和删除策略

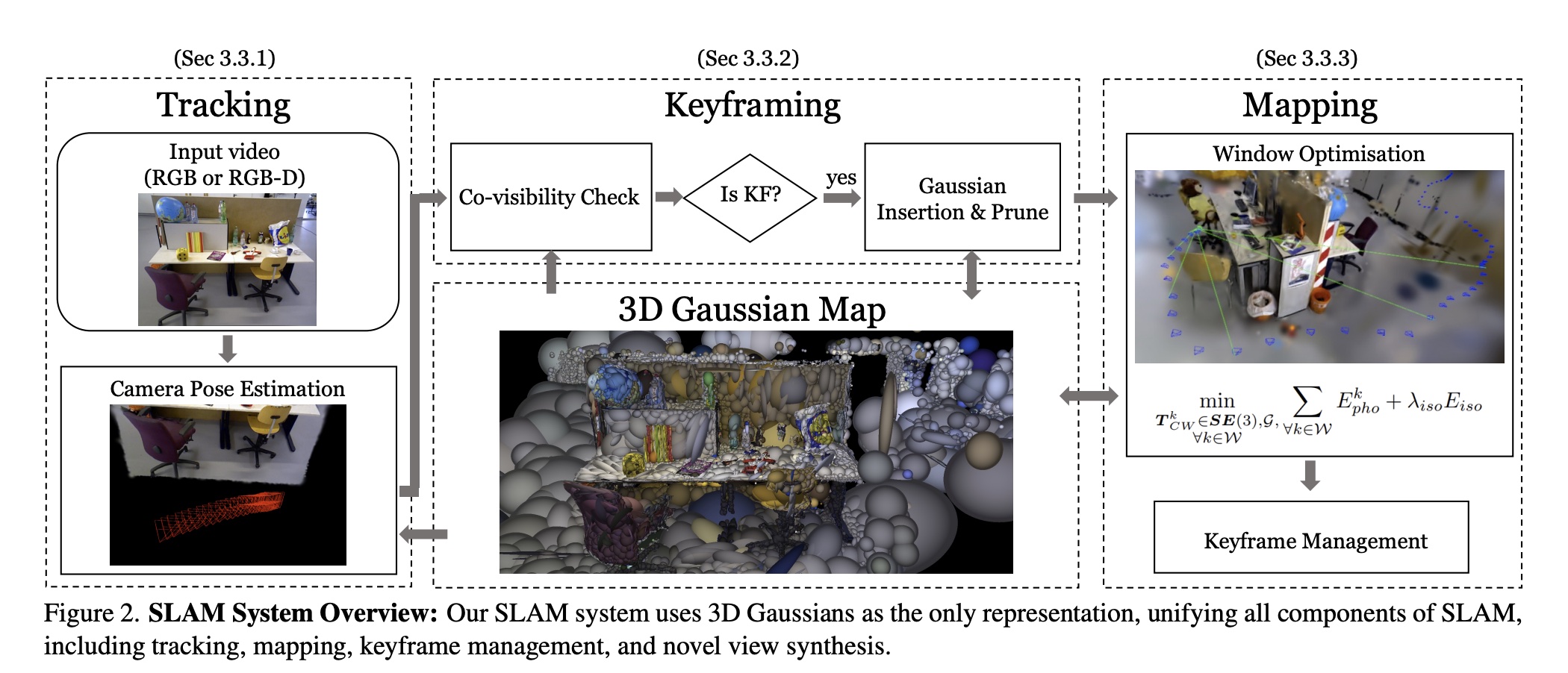
Gaussian Representation

用一组各向异性的高斯 \(\mathcal{G}\) 映射场景 每个高斯值只有 8 个参数（RGB 3 个、中心位置 3 个、半径 1 个、不透明度 1 个）

Tracking

  • 估计相机外参 , 最小化以下目标函数
\[ \begin{aligned} E_{pho}=\left\|I(\mathcal{G},\boldsymbol{T}_{CW})-\bar{I}\right\|_{1}\\ E_{geo}=\left\|D(\mathcal{G},\boldsymbol{T}_{CW})-\bar{D}\right\|_{1} \\ \min \lambda_{pho} E_{pho} + (1 - \lambda_{pho})E_{geo} \end{aligned} \]

parameters

  • \(\lambda_{pho}\) 权重超参数
  • \(I(\mathcal{G},\boldsymbol{T}_{CW})\) 表示从外参为 \(\boldsymbol{T}_{CW}\) 的相机渲染高斯集合 \(\mathcal{G}\) 所得的图片
  • \(\bar{I}\) 真实图片
  • \(E_{pho}\) 图片误差
  • \(E_{geo}\) 深度误差 , 仅在深度信息可用时引入
  • \(D(\mathcal{G},\boldsymbol{T}_{CW})\) 渲染出来的深度（渲染方式和 RGB 值类似 , 均为按不透明度和透光率加权平均）
  • \(\bar{D}\) 深度数据

Keyframing

  • 选取关键帧窗口 \(\mathcal{W}_k\), 两帧之间共同可见 Gaussian 的比例
    • 判断 Gaussian 是否可见的方法就是判断到该 Gaussian 的透光率是否达到 0.5
  • 定义共同可见度（covisibility）为当前帧 \(i\) 与上一关键帧 \(j\) 之间可见 Gaussian 集合的 IoU
  • 若 covisibility 低于某个阈值，或相对平移 \(t_{ij}\) 相对于深度中位数较大，则帧 \(i\) 被视为关键帧
  • 同时在当前帧 \(i\) 被加入到关键帧窗口时，也要移除 \(\mathcal{W}_k\) 中老旧的关键帧
    • 当帧 \(j \in \mathcal{W}_k\) 与当前帧 \(i\) 可见 Gaussians 的重叠系数 OC 小于某个阈值时，移除。
\[ OC_{cov}(i,j)=\frac{|\mathcal{G}_i^v\cap\mathcal{G}_j^v|}{\min(|\mathcal{G}_i^v|,|\mathcal{G}_j^v|)} \]

Gaussian Insertion and Pruning

  • 每个关键帧都会添加新的 Gaussians，用关键帧的每个像素点的深度 D（在单目相机的情况下会渲染深度来估计 D 的值）作为新增 Gaussians 的参考位置
  • 由于 D 不一定准确，新的 Gaussians 的深度服从一个均值为 D、方差较小的正太分布
  • 对于没有深度估计的像素，新 Gaussians 的深度服从均值为渲染图像深度中位数、方差较大的正太分布
  • 一开始没有 Gaussian 时，新增 Gaussian 的位置是随机的
  • 当关键帧窗口 \(\mathcal{W}_k\) 已满，执行剪枝操作，如果最近三个关键帧那新增的 Gaussians 没有在其他至少三帧内观察到，移除。不透明度小于 0.7 的 Gaussians 也会被移除。

Mapping

  • 维护一个协调的 3D 结构并优化新插入的 Gaussians
  • 参与优化的帧集合为 \(\mathcal{W}=\mathcal{W}_k \cup \mathcal{W}_r\)，其中 \(\mathcal{W}_r\) 是随机选取的两个旧帧
  • 3D 高斯渲染过程中没有对沿光线方向的 Gaussian 进行约束，会导致 SLAM 过程中出现伪影，因此引入各向同性约束
\[ E_{iso}=\sum_{i=1}^{|\mathcal{G}|}\left\|\mathbf{s}_i-\tilde{\mathbf{s}_i}\cdot\mathbf{1}\right\|_1 \]
  • 对于建图部分，最小化以下目标函数
\[ \min_{\boldsymbol{T}_{CW_{\forall k\in\mathcal{W}}}^k\in\mathbf{SE}{(3),\mathcal{G}}}\sum_{\forall k\in\mathcal{W}}E_{pho}^k+\lambda_{iso}E_{iso} \]

Experiments

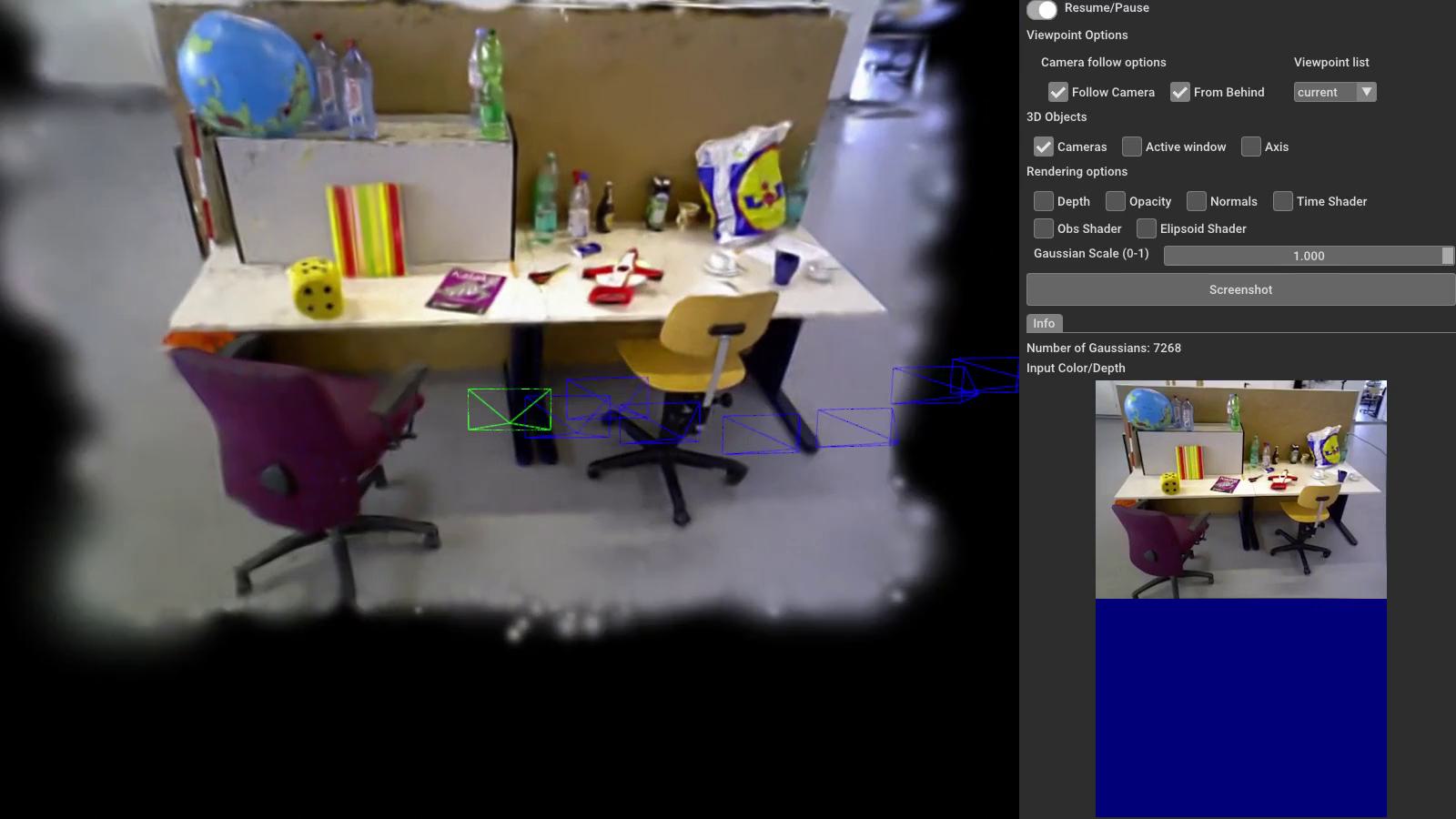
Reference

最后更新: 2024年10月13日 15:51:16
创建日期: 2024年10月13日 15:51:16
回到页面顶部