VGGT-Long¶

Introduction¶

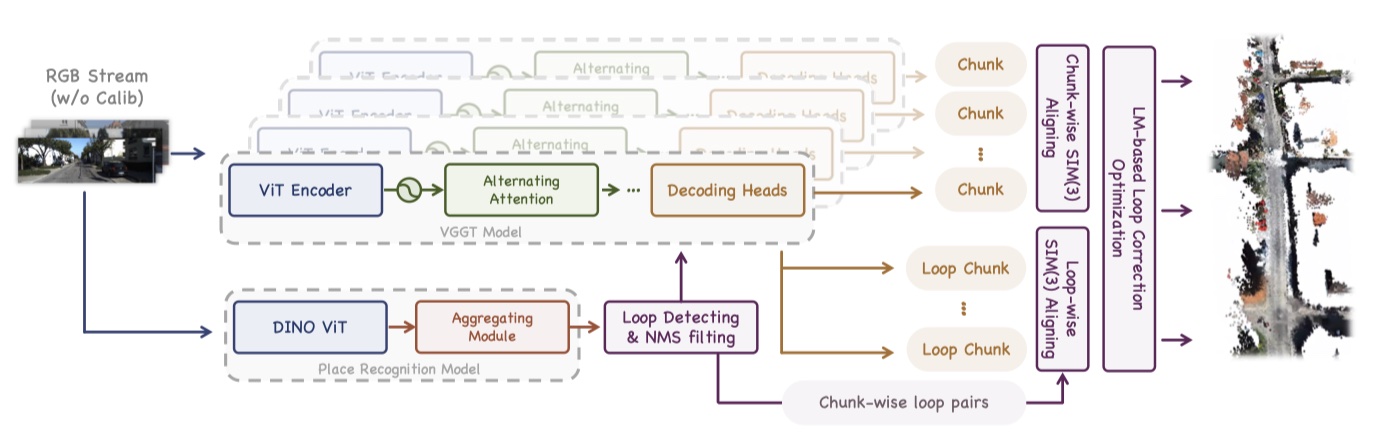
Method¶

Sequence Chunking and Local Aligning with Confidence¶

分块处理 ¶

• 给定长序列，按照窗口长度 L 和重叠长度 O 进行滑动切块；
  • 第 k 个块 \(C_k\) 包含帧 : \(C_k = \{I_{(k-1)(L-O)}+1, ..., I_{(k-1)(L-O)+L}\}\)
• 每个 chunk 被单独输入到 VGGT 中，输出：
  • 每帧的相机位姿；
  • 稠密点云 \(P_k\)；
  • 每个点的置信度 \(c_k\)；
• 由于每段都不长，并且有重叠，所以可以进行对齐与拼接。

基于置信度的 SIM(3) 对齐 ¶

• 对每对相邻 chunk \(C_k\) 与 \(C_{k+1}\)：

  • 找到在重叠区域中的 3D 点对 \((p_k^i, p_{k+1}^i\)；
  • 使用加权的 IRLS 算法优化 SIM(3) 变换；
  \[ \mathbf{S}_{k,k+1}^*=\arg\min_{\mathbf{S}\in\mathrm{Sim}(3)}\sum_i\rho\left(\|\mathbf{p}_k^i-\mathbf{S}\mathbf{p}_{k+1}^i\|_2\right) \]

• 使用加权 Umeyama 算法求解 SIM(3)；

• 策略细节：
  • 置信度低于 chunk 中值 10% 的点直接丢弃；
  • 中置信度（缓慢的车辆）赋较低权重；
  • 高置信度主导对齐；
  • 滤出动态物体、天空等非稳定区域；

Loop Detection and Loop-wise SIM(3) Aligning¶

Loop Detection¶

• 使用预训练的 DINOv2 提取每帧的 global feature；
• 基于余弦相似度 + 时间距离 \(\Delta t > t_{\min}\) 进行最近邻匹配；
• 应用 NMS，避免重复或近时序匹配；
• 得到高置信度图像级闭环对 \((I_i,I_j)\)。

构造“闭环 chunk”，实现几何约束 ¶

• 对于闭环对 \((I_i,I_j)\)，提取以 i, j 为中心的子序列各一段，组成新 batch；
• 用 VGGT 再次处理，构造“闭环 chunk”点云；
• 将该 chunk 对齐到原始 \(C_i\) 和 \(C_j\)，得到 \(S_{i, loop}, S_{j, loop}\)；
• 闭环配准为 \(S_{j, i} = S_{j, loop} \cdot S_{i, loop}^{-1}\)；

Global SIM(3) LM-based Optimization¶

• 为了获得全局一致性的轨迹和点云结果，执行 SIM(3) 空间下的全局 LM 优化：
• 优化变量：每个 chunk 对应的一个位姿变换 \(S_k \in Sim(3)\)；
• 优化目标函数：
  • 相邻块对齐约束：\(\arg\min_{\{\mathbf{S}_k\}}\sum_{k=1}^{K-1}\|\log_{\mathrm{Sim}(3)}(\mathbf{S}_{k,k+1}^{-1}\mathbf{S}_k^{-1}\mathbf{S}_{k+1})\|_2^2\)
  • 闭环约束：\(\sum_{(i,j)\in\mathcal{L}}\|\log_{\mathrm{Sim}(3)}(\mathbf{S}_{ij}^{-1}\mathbf{S}_i^{-1}\mathbf{S}_j)\|_2^2\)
• 解法：
  • 将 Sim(3) 映射到李代数 sim(3) 的 7D 切空间；
  • 使用 LM 算法求解；
  • Python 版本每步 3-13 ms，C++ 仅 0.4-1.3 ms；
  • 通常 3 步收敛。

Experiments¶

Reference¶

• 【论文精读】VGGT-Long