D\(^4\)Recon¶
约 1400 个字 1 张图片 预计阅读时间 5 分钟
Abstract
DIntroduction¶
问题导向
当前方法在高保真重建不可逆组织变形方面存在困难。
解决方案
- 在 Dynamic-3DGS 中提出双阶段变形建模和双尺度深度引导 D\(^4\)，并结合 MLP 对内窥镜场景中的动态进行建模；
- 在双阶段变形建模中，引入空间变形模型来矫正多视图不一致性，时间变形模型来准确表示参考帧中组织的扭曲以及组织与手术工具的动态交互；
- 在双尺度深度引导中，提出平衡局部误差矫正与绝对深度一致性，从而在保留细粒度颜色准确性的同时实现精确的深度细化；
Method¶
Dynamic 3D Scene Representation¶
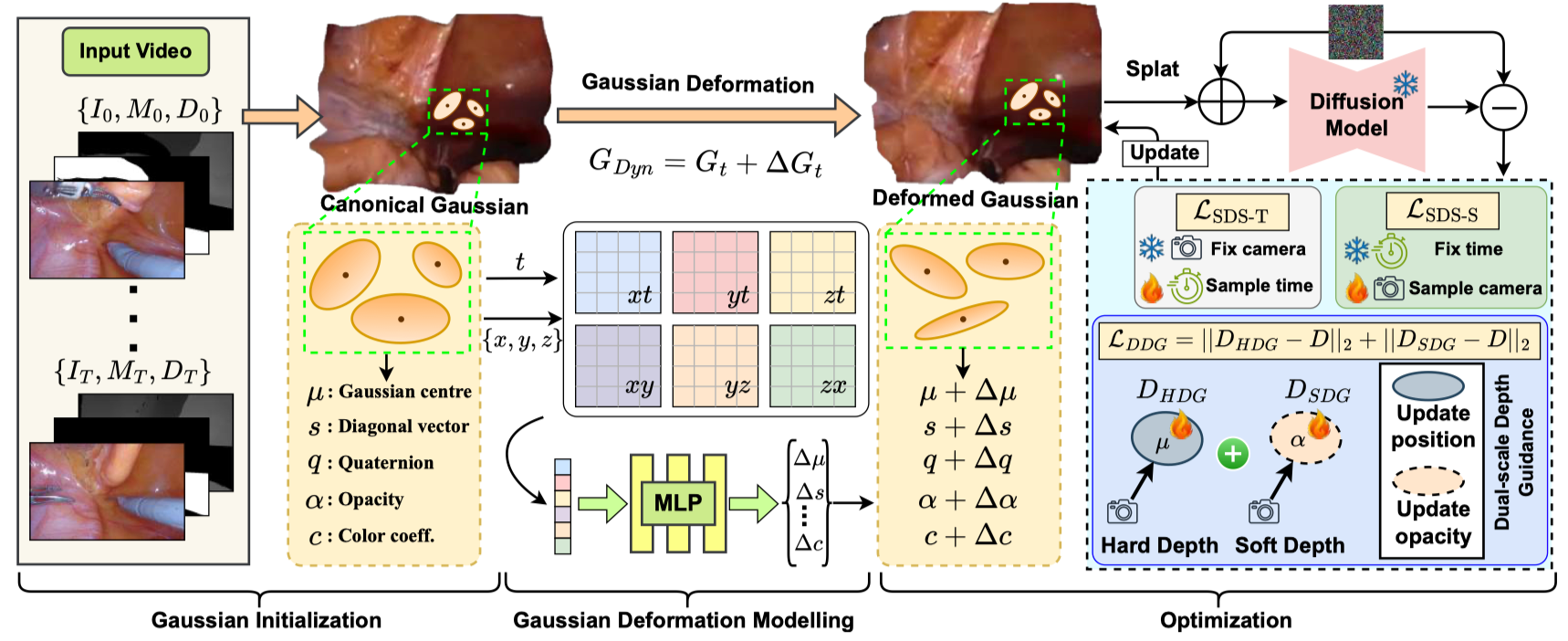
Gaussian Initialization¶
- 从第 0 帧将组织像素投影到 3D 空间以创建初始点云；
- 为解决手术工具遮挡问题，从后续帧更新组织像素信息，生成优化后的 \((I^\prime, D^\prime, M^\prime)\)：对于每个像素 \(p\)，如果第 0 帧的 \(M_0(p)=1\)，而第 \(t\) 帧的 \(M_t(p)=0\)，则用第 \(t\) 帧的值更新 \(I^\prime\) 和 \(D^\prime\)，否则保留第 0 帧的数据，优化后的点云 \(P^\prime\) 为：
\[
P^\prime = \{D^\prime K_e^{-1}K_i^{-1}(I^\prime \odot (1-M^\prime))\}, \quad M^\prime = \cap_{\tau=0}^t M_\tau
\]
Dynamic Gaussian Representation¶
类似 4DGS。
Dual-scale Depth Guidance¶
- 3DGS 对四个参数 \(\{\mu, s, q, \alpha\}\) 进行优化，然而单目深度比颜色更平滑，对所有参数进行统一正则化可能会导致过拟合和模糊，为了同时保持几何保真度和视觉清晰度，仅对 \(\{\mu, \alpha\}\) 进行正则化（这两个参数是空间位置和占有率的主要决定因素，同时保持 \(s\) 和 \(q\) 固定，以避免引入颜色重建伪影
） ； - 为了增强高斯场，引入硬深度引导（HDG），利用高斯中心 \(\mu\) 中编码的全局深度线索；为所有高斯分配一个高不透明度 \(\beta\) 并主要从沿像素 \(p\) 投射的光线中最接近相机中心 \(\rho\) 的高斯渲染出硬深度 \(D_{HDG}\)，从而确保全局深度一致性：
\[
D_{HDG}(p) = \sum_{i} \beta (1 - \beta)^{i-1} \| \rho - \mu_i \|_2
\]
- 硬深度引导缺乏不透明度优化，可能导致半透明表面和空洞结构，所以冻结 \(\mu\) 以防止不期望的偏移，并引入软深度引导（SDG）来优化 \(\alpha\)，同时保持几何结构，这利用 \(\alpha\) 通过不透明度控制局部深度线索：
\[
D_{SDG}(p) = \sum_{i} \alpha_i^\prime \prod_{j=1}^{i-1} (1 - \alpha_j^\prime) \| \rho - \mu_i \|_2
\]
- 使用 \(L_2\) 损失来加强与单目深度的对齐：
\[
\mathcal{L}_{DDG}(p) = \| D_{HDG}(p) - D_{SDG}(p) \|_2 + \| D_{SDG}(p) - D(p) \|_2
\]
Dual-stage Deformation Modeling¶
传统 3DGS 通常依赖手工设计的深度启发式方法，难以解决多视图不一致带来的固有场景模糊问题（例如，非朗伯表面、瞬态遮挡
提出一种变形框架，通过两个新颖的分数蒸馏采样（SDS）目标来分离几何和时间上的细化，该框架利用了预训练的 2D Diffusion Model 的语义和结构先验
为减轻多视图冲突和时间闪烁，引入两个变形场：
- 空间变形场 \(\mathcal{D}_s\)，用于调整高斯位置已解决静态的多视图不一致问题；
- 时间变形场 \(\mathcal{D}_t\)，用于建模跨时间的动态场景变化；
这些场通过 SDS 损失进行联合优化，既与扩散先验保持一致，又能保持物理合理性。
Multiview Consistency¶
- 为进行空间细化，从规范轨迹分布中采样一个相机位姿 \(\hat{P}_i\)，冻结时间 \(t\)，并通过 render 渲染得到 \(\mathcal{I}_{\hat{P}_i}\)，并用高斯噪声扰动 \(\mathcal{I}_{\hat{P}_i}\) 得到 \(\mathcal{I}_{\hat{P}_i}^\epsilon\)，并计算噪声残差 \(\epsilon_\phi\)（\(\phi\) 是冻结的 diffusion weights
） ； - 空间 SDS loss \(\mathcal{L}_{SDS-S}\) 通过 \(\mathcal{D}_s\) 反向传播梯度：
\[
\cap \rho \epsilon \nabla_{\theta_{s}} \mathcal{L}_{\mathrm{SDS}-\mathrm{S}}=\mathbb{E}_{\hat{P}_{i}, \epsilon, \sigma}\left[w(\sigma)\left(\epsilon_{\phi}-\epsilon\right) \frac{\partial \mathcal{I}_{\hat{P}_{i}}}{\partial \theta_{s}}\right] ; \epsilon_{\phi}=\operatorname{Diffusion}\left(\mathcal{I}_{\hat{P}_{i}}^{\epsilon}, \hat{P}_{i}, \sigma\right)
\]
Temporal Consistency¶
- 为防止退化的空间解（例如 flatness
） ，应用时间 SDS loss \(\mathcal{L}_{SDS-T}\)，以增强在采样时间步长 \(t \sim [t_0 - \Delta t, t_0 + \Delta t]\) 上的连贯性； - \(D_t\) 将高斯分布变形到位置 \(\mu + \mathcal{D}_t(\mu, t)\)，\(\mathcal{L}_{SDS-T}\) 在渲染动态序列时会惩罚与扩散先验的偏差；
- 空间场和时间场是交替优化的，这将高频几何细节（由 \(\mathcal{D}_s\) 处理）与低频运动（由 \(\mathcal{D}_t\) 处理）分离开来。
与传统的 SDS（仅简单地蒸馏单视角语义）不同
- 方法明确地对真实世界场景的静态 - 动态二元性进行建模，并且在扩散模型中利用相机位姿来解决 SDS 中的不一致性；
- 将总损失表示为 \(\mathcal{L}_{\text {total }}=\mathcal{L}_{D D G}+\mathbb{1}_{k} \mathcal{L}_{\mathrm{SDS}-\mathrm{S}}+\left(1-\mathbb{1}_{k}\right) \mathcal{L}_{\mathrm{SDS}-\mathrm{T}}\)，迭代 \(k\) 次时，\(G_{Dyn}^{k+1}\gets G_{Dyn}^k-\eta\nabla\mathcal{L}_{total}\)。
与 4DGS 在单一体积表示中对时空进行参数化不用
- 方法初始化每帧高斯分布，并通过具有双尺度深度引导的局部时空更新来对齐，因此为 Dynamic-3DGS。