Endo-4DGS¶

Introduction¶

解决方案

4DGS 捕捉时间动态，Depth-Anything 生成伪深度图并作为几何先验；同时提出置信度引导学习，解决单目深度估计位姿估计不准确问题，并通过表面法向约束和深度正则化来增强深度引导的重建效果。

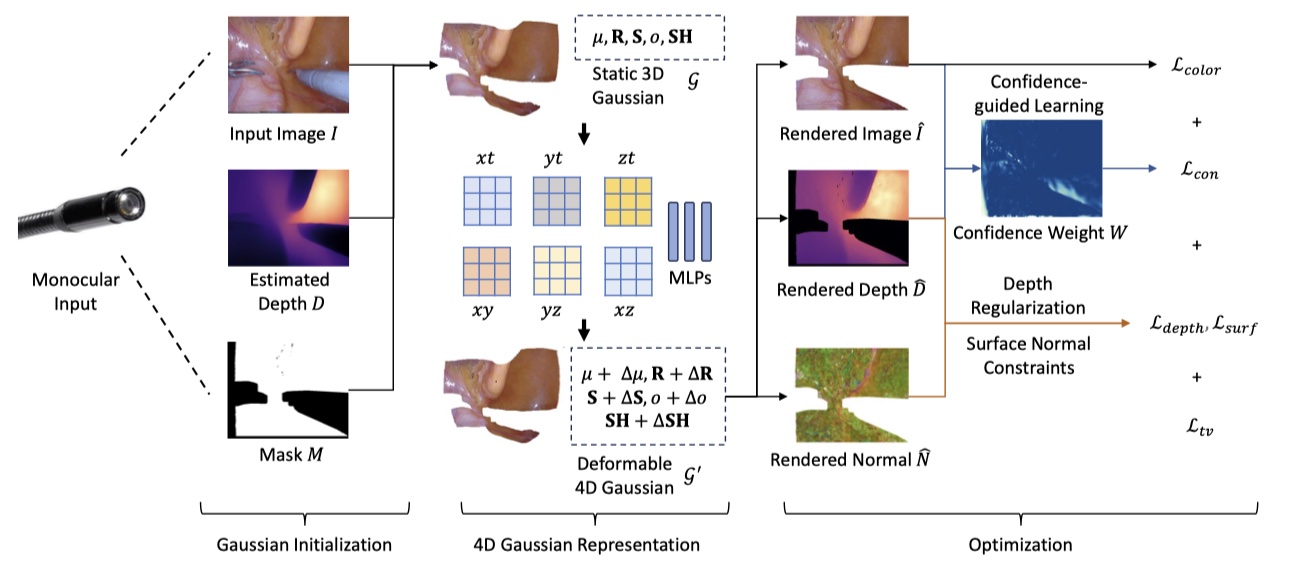
Method¶

4DGS for Deformable Scene Representation¶

• 用 4D Gaussian \(\mathcal{G}^\prime = \Delta \mathcal{G} + \mathcal{G}\) 表示可变性的手术场景，其中包括静态 3D Gaussian \(\mathcal{G}\) 以及变形 \(\Delta \mathcal{G} = \mathcal{F}(\mathcal{G}, t)\);
• 时空编码器 \(\mathcal{H}\) 由多分辨率六平面和一个小型 MLP 组成（K-Plane），\(\mathcal{H}(\mathcal{G},t)=\{ R_l(i,j), \phi_d | (i,j) \in \{ (x,y),(x,z),(y,z),(x,t),(y,t),(z,t) \}, l \in \{1,2\} \}\)，并且时空特征被编码为 \(f_d = (\mathcal{H}(\mathcal{G}, t))\);
• 用一个 multi-head Gaussian deformation decoder \(\mathcal{D} = \{ \phi_\mu, \phi_r, \phi_s, \phi_o, \phi_{\mathbf{SH}} \}\)，对五个参数进行解码，4D Gaussian 最终表示为：

Gaussians Initialization with Depth Prior¶

• 利用 Depth-Anything 实现 4D Gaussian 的点云初始化 ;
• 利用模型估计出逆深度图 \(D_{inv}\)，然后应用缩放因子 \(\beta\) 来恢复相机坐标系下的深度图 \(D=\frac{\beta}{D_{inv}}\);
• 给定相机内参 \(K_1\) 和外参 \(K_2\)，将大小为 \(N\) 的点云 \(P \in \mathbb{R}^{N \times 3}\) 从给定的图像 \(I\) 中投影：

Confidence Guided Learning¶

• 由于无法获取真实的几何信息，基于估计深度的单目重建是一个不适定问题，所以构建一个概率模型来从 Depth-Anything 中学习深度的统计信息：

• 置信引导损失，在可信度较低的深度和颜色进行惩罚的同时，还添加了 \(\log(\cdot)\) 作为正则项。置信权重会在渲染深度与深度先验不同的地方最大化误差，同时减少预训练深度估计中的不确定值的影响：

Surface Normal Constraints and Depth Regularization¶

• 为了更有效地将预训练的深度图作为伪真值，提出使用深度正则化损失和表面法向量损失；

• 表面法向量损失：

  • 用最短轴近似表面法向量 \(\hat{n}_i \in \hat{\mathbf{N}}\)：
  \[ \hat{\mathbf{n}}_\mathbf{i} = \mathbf{R}_i[r:], \quad r = \argmin([s_1, s_2, s_3]) \]
  • 计算深度先验的梯度 \(\bigtriangledown D = (G^W, G^H)\)，其中 \(G^W, G^H\) 是沿深度图宽度和高度的梯度，并将伪表面法向量表示为：
  \[ \mathbf{n}_i=\left [ \frac{G_i^W}{\sqrt{(G_i^W)^2+(G_i^H)^2+1}},\frac{G_i^H}{\sqrt{(G_i^W)^2+(G_i^H)^2+1}},\frac{1}{\sqrt{(G_i^W)^2+(G_i^H)^2+1}} \right ] \]
  • 表面法向量约束为 \(\mathcal{L}_{surf} = \| \mathbf{N} - \hat{\mathbf{N}} \|_1\)

• 深度正则化损失：

  • 通过归一化深度损失和梯度损失来正则化 4D Gaussian 预测的深度：
  \[ \mathcal{L}_{depth} = \lambda_{norm} \| D_{norm} - \hat{D}_{norm} \|_1 + \lambda_{grad} (1 - P_{corr}(\| \bigtriangledown D \|_2, \| \bigtriangledown \hat{D} \|_2)) \]
  • \(P_{corr}(\cdot)\) 是皮尔逊相关系数 ;

• 结合颜色损失 \(\mathcal{L}_{color}\) 和基于网格的总变分损失 \(\mathcal{L}_{tv}\)，最终用于优化的损失函数为：

Experiments¶

Reference¶

• [ 论文审查 ] Endo-4DGS: Endoscopic Monocular Scene Reconstruction with 4D Gaussian Splatting