EndoGaussian¶
约 971 个字 3 张图片 预计阅读时间 3 分钟
Abstract
Introduction¶
问题导向
- NeRF 渲染速度慢,限制在实际应用中的可行性;
- 3DGS 中的高斯初始化策略(SFM/COLMAP
) ,由于组织变形和光照变化,无法生成密集且准确的点,3DGS 的学习过程在很大程度上依赖于初始化点的数量和准确性; - 原始 3DGS 是为静态场景设计的,如果采用 MLP 来跟踪每个高斯的动态,MLP 缺乏从输入中明确编码时空关系的固有能力,很难应用到内窥镜中。
解决方案
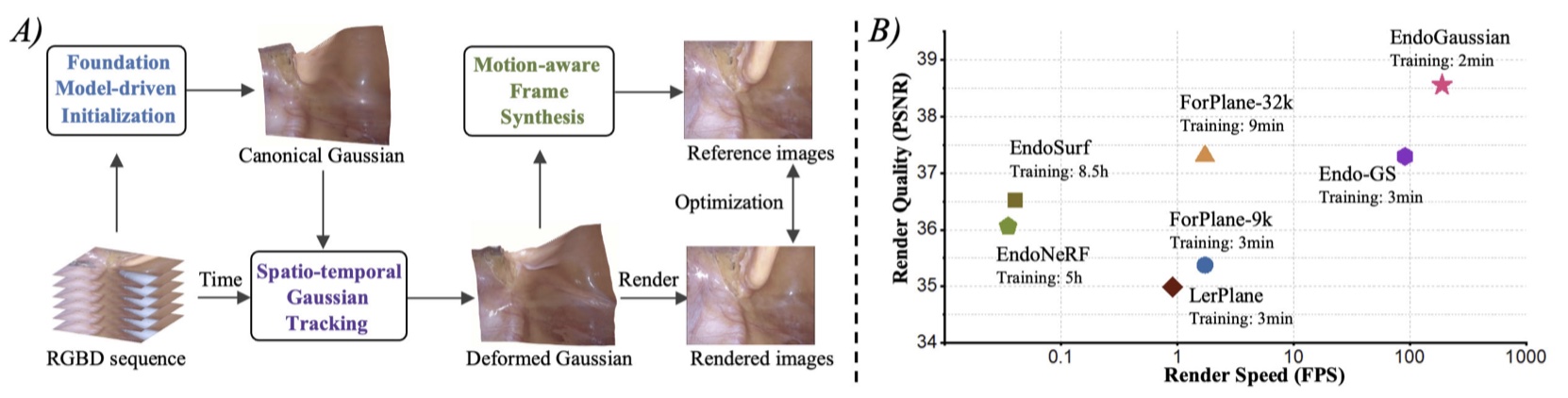
提出 EndoGaussian 框架,整合了 3DGS 的优势,实现高保真度的组织重建、高效训练和实时渲染;
Method¶
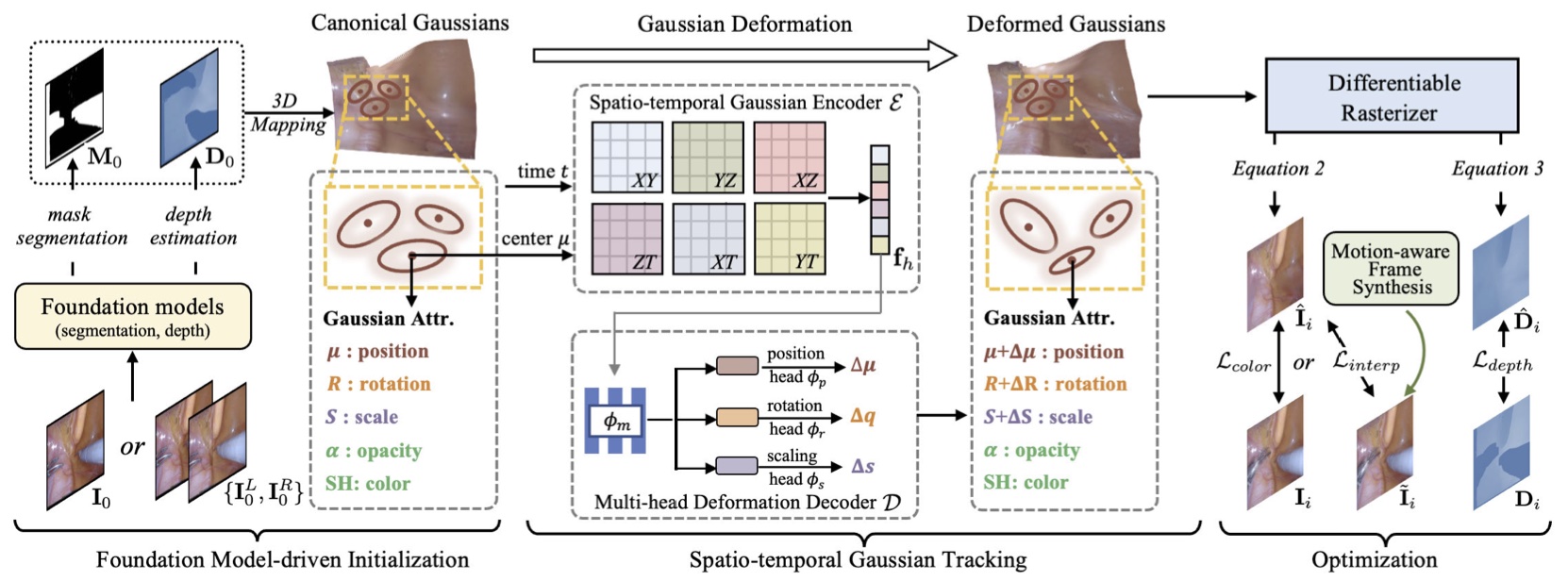
Foundation Model-Driven Initialization (FMI)¶
- Instrument Mask Segmentation:使用 Grounded-SAM(Grounded-DINO + SAM)生成器械掩码;
- Depth Map Estimation:单目使用 Depth Anything Model(DAM
) ,双目使用 STTR; - 3D Mapping for Gaussian Initialization:\(P_i = K^{-1} T_i D_i(I_i[M_i=1])\)
Spatio-Temporal Gaussian Tracking (SGT)¶
- 将形变场拆分为 \(\mathcal{F} = \mathcal{D} \circ \mathcal{\varepsilon}\),\(\mathcal{\varepsilon}\) 是时空高斯编码器,\(\mathcal{D}\) 是多头属性解码器;
- Spatio-Temporal Gaussian Encoder:借鉴 4DGS;
- Multi-Head Attribute Decoder:\(f_m=\phi_m(f_h)\) 整合来自不同分辨率尺度的信息,multi-heads decode 将融合后的特征解码为位置偏移、旋转偏移和尺度偏移(不对不透明度和 SH 的偏移解码
) ;
Motion-Aware Frame Synthesis (MFS)¶
大幅度运动组织变形
虽然形变场能对表面动态进行建模,但当组织运动幅度较大时,会遇到渲染模糊的问题。 因为形变场缺乏足够的约束,而用于快速组织运动的训练图像数量稀少,无法提供充分的训练约束。
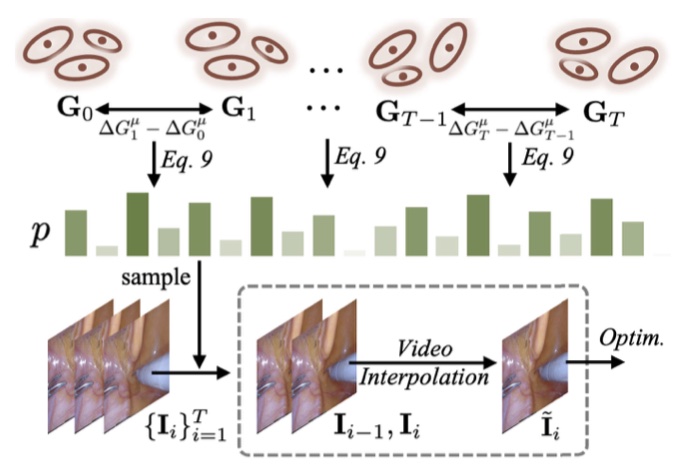
- 为了在组织运动较大的时间间隔处合成图像,首先估计每个间隔的运动程度;
- 对高斯分布和形变场 \(T_p\) 次迭代的预训练后,计算每个间隔的偏移量 \(\{u_i \in R^{N \times 3} |u_i = \Delta G_i^\mu - \Delta G_{i-1}^\mu, i \in [1, T]\}\),并计算 \(u_i\) 的范数,对所有间隔的结果进行归一化,\(\{p_i | p_i = C \sum_j \| u_i^j \| / N, i \in [1, T]\}\);
- \(p_i\) 越大表示该区域具有较大运动的概率越高,基于 \(\{p_i\}_{i=1}^T\),对区间 \(R_i = [i-1, i]\) 进行采样,并采用实时视频插值模型 \(RIFE\) 在该区间的中点 \(\frac{i-1+i}{2}\) 处合成新帧;
- 除了合成图像,还需要工具掩码在优化过程中过滤无效的工具像素,由于变形在时间上往往具有方向一致性,所以取输入中相邻工具掩码的交集;
Optimization¶
- Color Loss:\(\mathcal{L}_{color} = \frac{1}{HW} \sum_p M_i(p) \cdot |\hat{I}_i(p) - I_i(p)|\)
- Depth Loss:\(\mathcal{L}_{depth} = \frac{1}{HW} \sum_p M_i(p) \cdot |\hat{D}_i^{-1}(p) - D_i^{-1}(p)|\)
- Smoothness Loss,为了避免在工具遮挡区域出现 “黑洞” 或 “白洞”:\(\mathcal{L}_{smooth} = \frac{1}{HW} \sum_p (1-M_i(p)) \cdot \| \Delta^2 \hat{I}_i(p) \|\)
- Interpolated Color Loss,为具有大变形的时间间隔提供约束:\(\mathcal{interp}=\frac{1}{HW} \sum_p \widetilde{M}_i(p) \cdot |\widetilde{I}_i(p) - \hat{I}_i(p)|\)
 Foundation Model-Guided Gaussian Splatting for 4D Reconstruction of Deformable Tissues
Foundation Model-Guided Gaussian Splatting for 4D Reconstruction of Deformable Tissues