EndoGaussian¶

Introduction¶

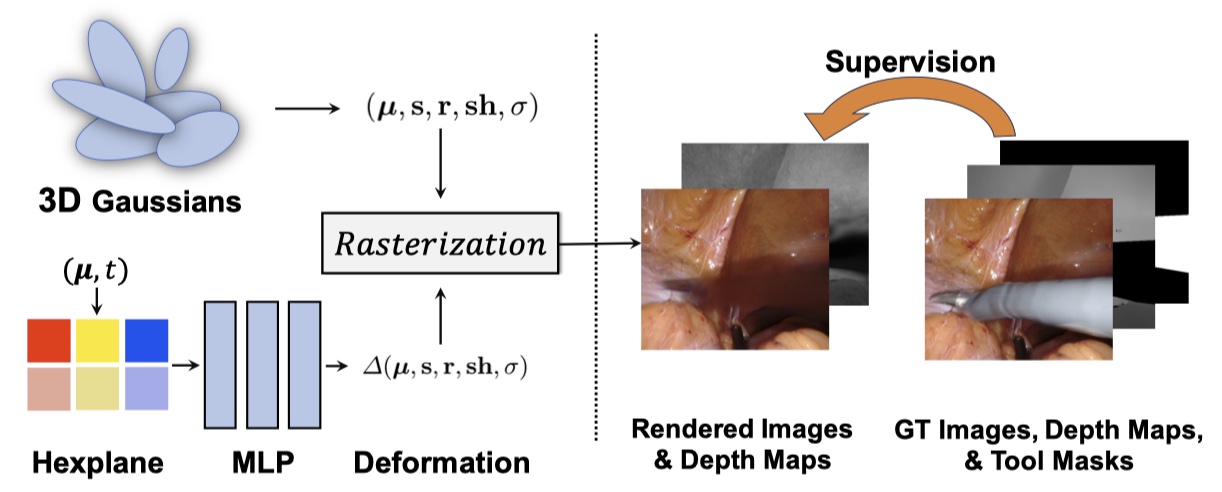
Method¶

Training Combined with Tool Masks and Depth Maps¶

• 使用标记的 \(M_i \in \{0, 1\}\) 表示工具遮挡；
• 引入时空重要性采样策略，指示与遮挡相关的关键区域；
• 重要性图 \(\mathcal{V}_i = (1-M_i) \odot \left ( 1 + \alpha \sum_{j=1}^T M_j / \left \| \sum_{j=1}^T M_j \right \|_F \right )\)；
• \(L_1\) 用于图像空间的监督：\(\mathcal{L}_{L1}(i)=|I_i \odot \mathcal{V}_i - \hat{I}_i \odot \mathcal{V}_i|\)；
• 使用估计的深度图引入深度引导损失，采用 Huber 损失 \(\mathcal{L}_D(i)\) 进行深度正则化；
• 使用空间和时间维度上的 Total Variation (TV) 损失作为额外的正则化项。

Surface-Aligned Gaussians¶

• 为了在三维线索有限的区域（特别是工具遮挡周围）减少伪影，为确保高斯分布与组织表面紧密结合，通过控制高斯分布的密度函数来进行表面对其归一化，可定义为 \(d(p) = \sum_g \sigma_g \exp (-\frac{1}{2}(p - \mu_g)^T \sum_g^{-1}(p-\mu_g))\)；
• 如果高斯分布与表面对其，可以做出三个假设：
  1. 离点 \(p\) 最近的高斯分布 \(g^* = \argmin_g \{(p-\mu_g)^T \sum_g^{-1}(p-\mu_g)\}\) 对密度 \(d(p)\) 的贡献最大；
  2. 为确保三维高斯分布是扁平的，每个高斯分布 \(g\) 的三个缩放因子中都有一个接近 0；
  3. 高斯分布是不透明的，可以通过交叉熵损失函数促使 \(\sigma_i\) 为 1； - 在这些假设下，可以将密度近似表示为 \(\tilde{d}(p)\)，并将理想距离函数近似为 \(f(p)\)；
• SDF 损失：\(\mathcal{L}_{SDF} = \frac{1}{\mathcal{P}} |\hat{f}(p) - f(p)|\)；
• 法线向量正则化：\(\mathcal{L}_{norm} = \frac{1}{\mathcal{P}} \sum_{p \in \mathcal{P}} \left \| \frac{\triangledown f(p)}{\|\triangledown f(p) \|_2} - n_{g^*}\right \|_2^2\)；
• 不透明度正则化项：\(\mathcal{L}_{opacity}(i) = -\sum_j (\sigma + \Delta \sigma)_j \log{\sigma + \Delta \sigma}_j\)；
• 总优化目标为：

Experiments¶

Reference¶

• [ 论文审查 ] EndoGS: Deformable Endoscopic Tissues Reconstruction with Gaussian Splatting