ST-Endo4DGS¶
约 617 个字 预计阅读时间 2 分钟
Abstract
Real-Time Spatio-Temporal Reconstruction of Dynamic Endoscopic Scenes with 4D Gaussian SplattingIntroduction¶
问题导向
现有方法难以应对内窥镜场景复杂的、随时间变化的动态特性。
解决方案
- 提出 ST-Endo4DGS，利用无偏的 4DGS 基元来建模动态内窥镜场景的时空体积，这些基元由具有灵活 4D 旋转的各向异性椭圆参数化；
- 扩展了球谐函数来表示随时间变化的外观，实现对光照和视角变化的真实适应；
- 一种新的内窥镜法向对齐约束（ENAC）通过将渲染的法向与深度衍生的几何结构对齐，进一步提高几何保真度。
Method¶
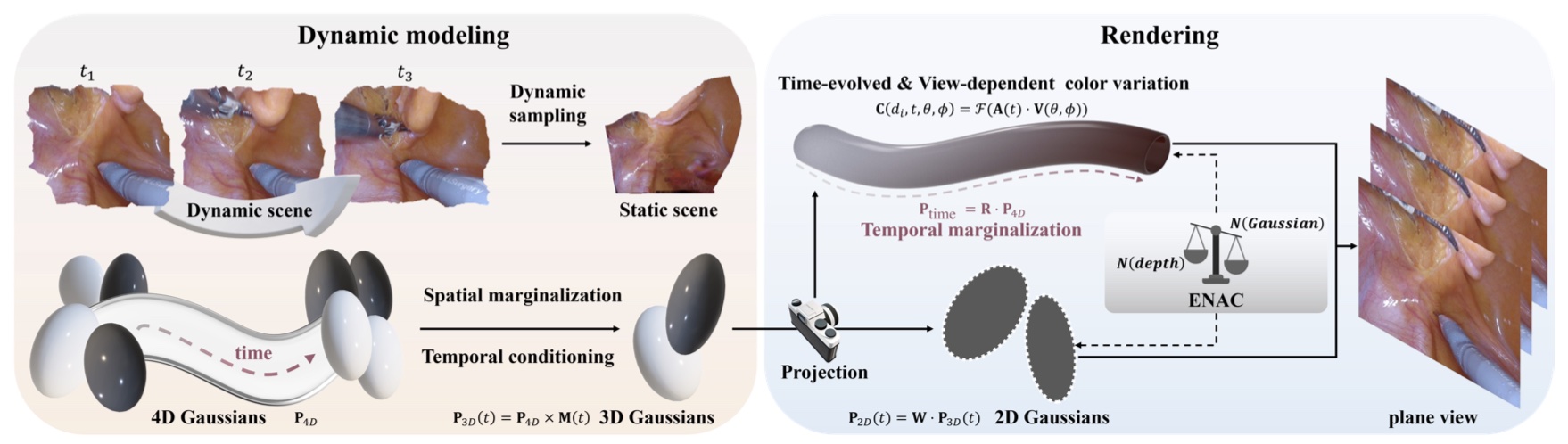
Spatio-temporal modeling with 4DGS¶
- 将 4D 表示简化为随时间变化的 3D 空间模型：\(P_{3D}(t)=P_{4D} \times M(t)\);
- 通过边缘化深度分量，将时间条件化的 3D Gaussian 投影到图像平面上的 2D Gaussian：\(P_{2D}(t)= W \cdot P_{3D}(t)\);
- 为了对时间演变且依赖于视图的外观进行建模，将颜色变化 \(C(d_i, t, \theta, \phi)\) 定义为时间 \(t\) 和观察方向 \(d_i\) 的函数：\(C(d_i, t, \theta, \phi) = \mathcal{F}(A(t) \cdot V(\theta, \phi))\)，其中 \(A(t)\) 是随时间变化的系数矩阵，\(V(\theta, \phi)\) 表示观察方向，\(\mathcal{F}\) 捕捉时间变化与依赖于视图的光照效果之间的相互作用，该公式可以基于时间和视角动态调整外观 ;
- 时间边缘化通过将 4D 表示整合为时间边缘化分布，进一步优化高斯模型的时间方面：\(P_{time} = R \cdot P_{4D}\);
- 最终的渲染方程表示为：
\[
\mathcal{I} = \sum_{i=1}^n \alpha_i \cdot (W \cdot (P_{4D} \times M(t))) \cdot (R \cdot P_{4D}) \cdot \mathcal{F}(A(t) \cdot V(\theta, \phi))
\]
Time-evolved appearance with Endo SH¶
- 内窥镜球谐函数几函数重新定义：
\[
Z_{nl}^m(t,\theta,\phi)=Y_l^m(\theta,\phi)\cdot\sin\left(\omega_nt+\phi_n\right)
\]
Enhancing geometric fidelity with ENAC¶
- ENAC 通过将从渲染深度图中导出的法向量 N(depth) 与从高斯表示中导出的法向量 N(Gaussian) 对齐，提高几何保真度。引入一个 \(L_1\) 正则项：
\[
L_{ENAC} = | N(depth) - N(Gaussian) |_1
\]
- 平衡渲染保真度和几何一致性的整体优化目标，实现与真实表面法向量的更好对齐：
\[
L_{total} = L_{render} + \lambda_{ENAC} \cdot L_{ENAC}
\]
Experiments¶
Reference¶
最后更新:
2025年10月21日 21:45:31
创建日期: 2025年10月21日 21:45:31
创建日期: 2025年10月21日 21:45:31