三维空间刚体运动 ¶
约 2134 个字 34 行代码 1 张图片 预计阅读时间 8 分钟
Abstract
- 理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角
- 掌握 Eigen 库的矩阵、几何模块的使用方法
旋转矩阵 ¶
点、向量和坐标系 ¶
- 空间中的某点。其位置固定。若采用不同的坐标系描述,其坐标位置具体形式是不同的,但是表达的点是同一个点。
- 用线代表示,在一个线性空间中,找到该空间的一组基\((\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3)\),那么,任意向量 \(\mathbf{a}\) 在这组基下的坐标为 \(\mathbf{a}=[\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3][a_1,a_2,a_3]^\top=a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3\)
- 坐标系定义时,有右手系和左手系,通常采用右手系
-
向量有内积和外积。
- 内积:\(\mathbf{a}\mathbf{b}=\mathbf{a}^\top\mathbf{b}=\sum_{i=1}^3a_ib_i=|\mathbf{a}||\mathbf{b}|\cos(\mathbf{a}, \mathbf{b})\)
- 外积:
\[ \mathbf{a} \times \mathbf{b}= \begin{bmatrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{bmatrix} = \begin{bmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{bmatrix} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \mathbf{b} \overset{\Delta}{=} \mathbf{a}^\wedge \mathbf{b} \]- 其中符号 \(\wedge\) 称为反对称符号,\(\mathbf{a}^\wedge\) 为反对称矩阵(满足 \(\mathbf{A}^\top=-\mathbf{A}\)
) ,这样做的好处可以奖向量运算变为矩阵运算
坐标系间的欧氏变换 ¶
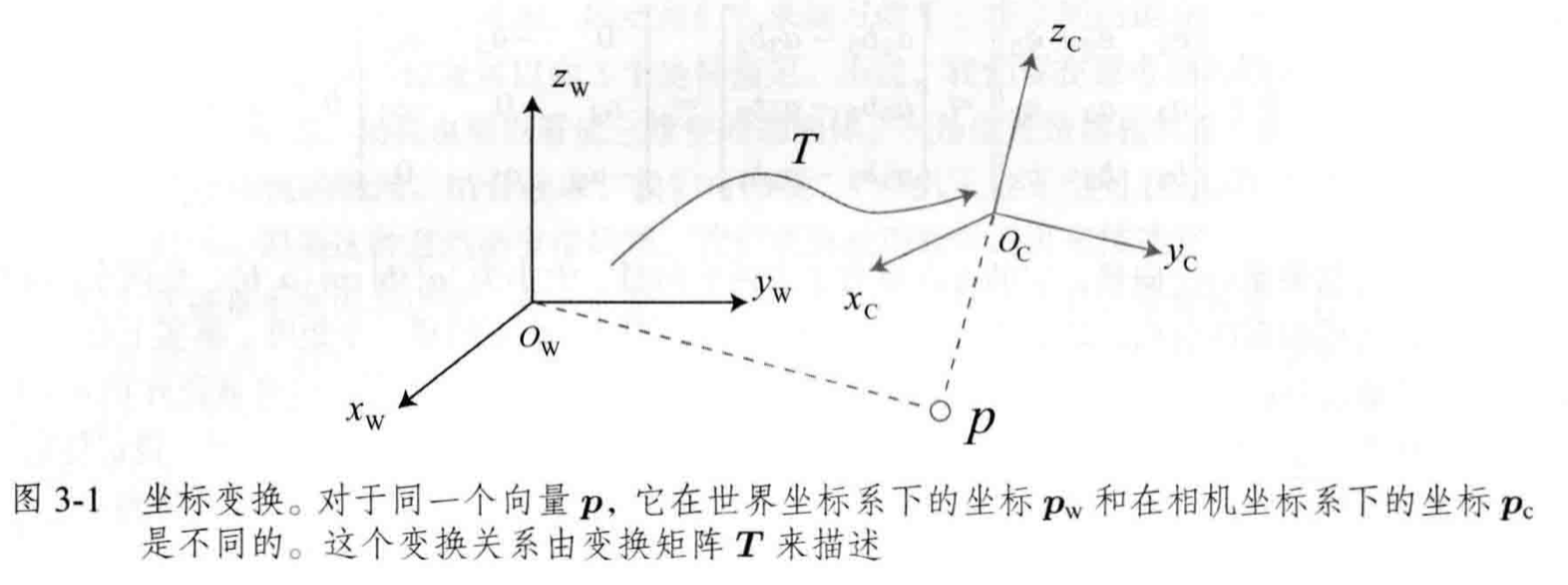
- 两个坐标系之间的运动由一个旋转加上一个平移组成,这种运动称为刚体运动,例如相机运动
- 刚体运动过程中,同一个向量在各个坐标系下的长度和夹角都不变,只会是空间位置和姿态不同,例如相机坐标系到世界坐标系,相差一个欧氏变换
-
欧氏变换由旋转和平移组成
-
旋转
- 设某个单位正交基 \((\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3)\) 经过一次旋转变成了 \((\mathbf{e}_1^\prime, \mathbf{e}_2^\prime, \mathbf{e}_3^\prime)\)。对于同一个向量 \(\mathbf{a}\) 没有随着坐标系的旋转而发生运动,所以
\[ [\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3]\begin{bmatrix}a_1 \\ a_2 \\ a_3 \end{bmatrix}=[\mathbf{e}_1^\prime, \mathbf{e}_2^\prime, \mathbf{e}_3^\prime] \begin{bmatrix} a_1^\prime \\ a_2^\prime \\ a_3^\prime \end{bmatrix} \\ 同时左乘 \begin{bmatrix} \mathbf{e}_1^\top \\ \mathbf{e}_2^\top \\ \mathbf{e}_3^\top \end{bmatrix}得 \ \ \ \begin{bmatrix}a_1 \\ a_2 \\ a_3 \end{bmatrix}=\begin{bmatrix} \mathbf{e}_1^\top \mathbf{e}_1^\prime & \mathbf{e}_1^\top \mathbf{e}_2^\prime & \mathbf{e}_1^\top \mathbf{e}_3^\prime \\ \mathbf{e}_2^\top \mathbf{e}_1^\prime & \mathbf{e}_2^\top \mathbf{e}_2^\prime & \mathbf{e}_2^\top \mathbf{e}_3^\prime \\ \mathbf{e}_3^\top \mathbf{e}_1^\prime & \mathbf{e}_3^\top \mathbf{e}_2^\prime & \mathbf{e}_3^\top \mathbf{e}_3^\prime \end{bmatrix}\begin{bmatrix}a_1^\prime \\ a_2^\prime \\ a_3^\prime \end{bmatrix}\overset{\Delta}{=}\mathbf{R}\mathbf{a}^\prime \]- 这里的 \(\mathbf{R}\) 是一个行列式为 1 的正交矩阵,由两组基之间的内积组成,所以矩阵 \(\mathbf{R}\) 描述了旋转本身,因此被称为旋转矩阵,同时也叫方向余弦矩阵
- 由于旋转矩阵为正交矩阵,它的逆(即转置)描述了一个相反的旋转,即 \(\mathbf{a}^\prime=\mathbf{R}^{-1}\mathbf{a}=\mathbf{R}^\top\mathbf{a}\)
-
平移
- \(\mathbf{t}\) 表示平移向量,其中 \(\mathbf{t}_{12} \ne -\mathbf{t}_{21}\),和两个系的旋转有关
- 旋转和平移合到一起:\(\mathbf{a}^\prime=\mathbf{R}\mathbf{a}+\mathbf{t}\)
- 实际中,定义坐标系 1 和坐标系 2,那么向量 \(\mathbf{a}\) 在两个坐标系下的坐标为 \(\mathbf{a}_1, \mathbf{a}_2\),它们之间的关系为 \(\mathbf{a}_1=\mathbf{R}_{12}\mathbf{a}_2+\mathbf{t}_{12}\),这里的 \(\mathbf{R}_{12}\) 是指“把坐标系 2 的向量变换到坐标系 1 中”
-
变换矩阵与齐次坐标 ¶
- 之前的变换关系不是线性关系
-
假设进行了两次变换,\(\mathbf{b}=\mathbf{R}_1\mathbf{a}+\mathbf{t}_1\) 和 \(\mathbf{c}=\mathbf{R}_2\mathbf{b}+\mathbf{t}_2\),那么 \(\mathbf{a}\) 到 \(\mathbf{c}\) 的变换为 \(\mathbf{c}=\mathbf{R}_2(\mathbf{R}_1\mathbf{a}+\mathbf{t}_1)+\mathbf{t}_2\),如果变换多次会变的非常繁琐,所以引入齐次坐标和变换矩阵
-
重写上式:
\[ \begin{bmatrix} \mathbf{a}^\prime \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^\top & 1 \end{bmatrix} \begin{bmatrix} \mathbf{a} \\ 1 \end{bmatrix} \overset{\Delta}{=} \mathbf{T} \begin{bmatrix} \mathbf{a} \\ 1 \end{bmatrix} \] -
在三维向量的末尾添加 1,将其变成了四维向量,称为齐次坐标。对于这个四维向量,可以把旋转和平移写在一个矩阵里,使得整个关系变成线性关系。其中矩阵 \(\mathbf{T}\) 称为变换矩阵
- 用 \(\tilde{\mathbf{a}}\) 表示 \(\mathbf{a}\) 的齐次坐标。所以通过齐次坐标和变换矩阵,两次变换的叠加就可以写成 \(\tilde{\mathbf{c}}=\mathbf{T}_2\mathbf{T}_1\tilde{\mathbf{a}}\)
-
旋转向量和欧拉角 ¶
- 旋转矩阵和变换矩阵都存在一个问题,就是变量的冗余。已知一次旋转仅有三个自由度,但是旋转矩阵有九个量,用九个量表示三个自由度(仅表示旋转
) ;变换矩阵有 16 个量,用 16 个量表示 6 个自由度(包括旋转和平移) 。 - 其次,旋转矩阵是一个特殊矩阵,即是正交矩阵,且行列式为 1。且该特殊性也会影响到变换矩阵,所以具有特殊性的矩阵在后续的非线性优化中会带来额外的约束,导致求解困难。
旋转向量 ¶
- 旋转向量 = 一个旋转轴 + 一个旋转角度即:旋转向量的方向为旋转轴,长度为旋转角度。
- 旋转向量和矩阵之间存在转换关系,用罗德里格斯公式(Rodrigues's Formula)表示:
\[
\mathbf{R}=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{n}\mathbf{n}^\top+\sin\theta\mathbf{n}^\wedge
\]
- 反之也可以计算从一个旋转矩阵到旋转向量的转换。对于转角 \(\theta\),取两边的迹,有
\[
tr(\mathbf{R})=\cos \theta \ tr(\mathbf{I})+(1-\cos \theta)tr(\mathbf{n}\mathbf{n}^\top)+\sin\theta \ tr(\mathbf{n}^\wedge) \\
tr(\mathbf{R})=3\cos\theta+(1-\cos\theta) \\
tr(\mathbf{R})=1+2\cos\theta \\
\theta = \arccos\left(\frac{tr(\mathbf{R})-1}{2}\right)
\]
- 关于转轴 \(\mathbf{n}\),旋转轴上的向量在旋转后不变,即 \(\mathbf{Rn}=\mathbf{n}\),因此转轴 \(\mathbf{n}\) 是矩阵 \(\mathbf{R}\) 特征值 1 对应的特征向量。
- 罗德里格斯公式详细推导
欧拉角 ¶
- 欧拉角是一种将旋转分解为三个基本旋转的方法,即绕三个坐标轴的旋转。欧拉角的表示方法有很多种,但是最常用的是Z-Y-X的旋转顺序,即先绕 Z 轴旋转,再绕 Y 轴旋转,最后绕 X 轴旋转。这种旋转顺序也叫航向 - 俯仰 - 滚转(yaw-pitch-roll
) 。 - 但是存在万向锁现象:万向死锁,所以使欧拉角在特殊情况下会出现奇异性。
四元数 ¶
四元数的定义 ¶
- 四元数是一种扩展复数的方法,复数由实部和虚部组成,而四元数由实部和三个虚部组成,即 \(\mathbf{q}=q_0+q_1i+q_2j+q_3k\),满足下面关系:
\[
\left\{\begin{matrix}
i^2 + j^2 + k^2 = -1 \\
ij = k, ji = -k \\
jk = i, kj = -i \\
ki = j, ik = -j
\end{matrix}\right.
\]
- 用一个标量和一个向量表示:\(\mathbf{q}=[s,\mathbf{v}],s=q_0 \in R, \mathbf{v}=[q_1,q_2,q_3]^\top \in R^3\),虚部为 0 为实四元数,实部为 0 为虚四元数
四元数的运算 ¶
- \(\mathbf{q}_a \pm \mathbf{q}_b = [s_a \pm s_b, \mathbf{v}_a \pm \mathbf{v}_b]\)
- \(\mathbf{q}_a \mathbf{q}_b=[s_as_b-\mathbf{v}_a^\top\mathbf{v}_b,s_a\mathbf{v}_b+s_b\mathbf{v}_a+\mathbf{v}_a\times \mathbf{v}_b]^\top\)
- \(\parallel \mathbf{q}_a \parallel = \sqrt{s_a^2+x_a^2+y_a^2+z_a^2}\)
- \(\mathbf{q}_a^*=s_a-x_ai-y_aj-z_ak=[s_a, -\mathbf{v}_a]^\top\)
- \(\mathbf{q}^{-1}=\mathbf{q}^*/\parallel \mathbf{q} \parallel^2\)
- \(k\mathbf{q}=[ks, k\mathbf{v}]\)
- \(\mathbf{q}_a \cdot \mathbf{q}_b=s_as_b+x_ax_bi+y_ay_bj+z_az_bk\)
用四元数表示旋转 ¶
- 三维空间点用一个虚四元数来描述:\(\mathbf{p}=[0,x,y,z]^\top=[0,\mathbf{v}]^\top\)
- 旋转后到点 \(\mathbf{p}^\prime\):\(\mathbf{p}^\prime=\mathbf{qpq}^{-1}\)
四元数到其他旋转表示的转换 ¶
- 轴角到四元数:\(\mathbf{q}=[\cos \frac{\theta}{2}, n_x \sin \frac{\theta}{2}, n_y \frac{\theta}{2}, n_z \sin \frac{\theta}{2}]^\top\)
- 四元数到轴角:\(\left\{\begin{matrix} \theta=2\arccos q_0 \\ [n_x,n_y,n_z]^\top=[q_1, q_2, q_3]^\top / \sin \frac{\theta}{2} \end{matrix}\right.\)
相似、仿射、射影变换 ¶
Eigen 库 ¶
install¶
Eigen 中矩阵的基本操作 ¶
Eigen::Matrix<type, row, colon> //typedef: Matrix3d, Vector3d...
Eigen::MatrixXd //unkown size matrix
matrix(i, j) //the value of i th row and j th colon
//the operations
matrix.transpose(); matrix.trace(); matrix.sum(); matrix.inverse(); matrix.determinant();
//find the proper values and vectors
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> solver(matrix.transport()*matrix);
solver.eigenvalues();
solver.eigenvectors();
//solve Matrix_NN * x = v_Nd
x = matrix_NN.colpivHouseholderQr().solve(v_Nd);
// 旋转向量和旋转矩阵
Eigen::AngleAxisd rotation_vector(theta, Eigen::Vector3d(x, y, z)); //rotation vector
rotation_matrix = rotation_vector.toRotationMatrix(); //transform rotation vector to rotation matrix
x_rotated = rotation_vector*x; //calculate rotated vector x'
x_rotated = rotation_matrix*x; //calculate rotated vector x'
// 四元数
q = Eigen::Quaterniond(w, x, y, z) //create a quaternion from four values
q = Eigen::Quaterniond(rotation_vector) //create a quaternion from rotaion vector
q = Eigen::Quaterniond(rotation_matrix) //create a quaternion from rotaion matrix
x_rotated = q * x //calculate rotated vector x'
// 变换矩阵 T
//create a transform matrix
Eigen::Isometry3d T = Eigen::Isometry3d::Identity();
T.rotate(rotation_vector);
/*
T.rotate(rotation_matrix);
T.rotate(quaternion);
*/
T.pretranslate(Eigen::Vector3d(x, y, z));