FastMAC¶
约 1447 个字 2 张图片 预计阅读时间 5 分钟
Abstract
Introduction¶
问题导向
MAC 面临着处理大量输入对应关系时效率低下的问题,无法满足实时的需求,而高精度配准问题与实时运行速度之间存在平衡。现有的随机采样方法(如最远点采样 FPS)虽然能加速配准过程,但会导致不稳定和性能下降,这是由于 MAC 基于对应关系图的最大团搜索,而传统的降采样方法无法维持利于最大团搜索的图结构。
解决方案
FastMAC 利用图信号处理技术,在对应关系图上提出了广义度信号,通过高频图滤波器过滤出广义度信号的高频分量,基于随机谱采样实现了对对应关系的降采样,在不降低性能的情况下,实现对 MAC 的 80 倍加速。
Method¶
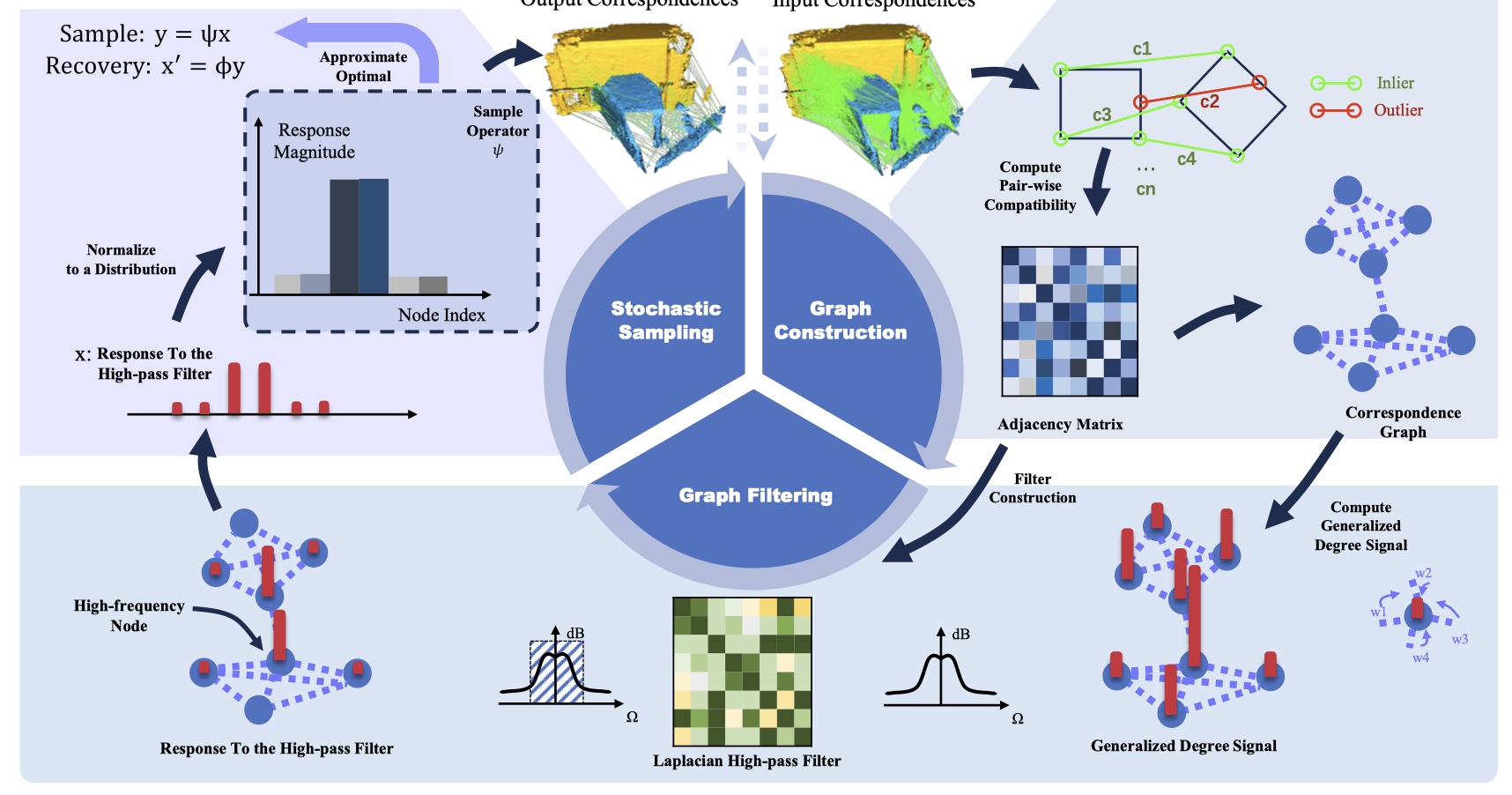
FastMAC(基于 MAC)一共 4 个步骤:
- Graph Construction
- Maximal Clique Search
- Node-guided Clique Selection
- Pose Estimation
广义度信号
- 为了引入图信号处理理论,需要在对应图上定义一个信号。
- 正常节点的度信号是它连接边的数量。
- 加权图中,节点的广义度信号为它连接的边的权重和。
Graph Filtering: Key Insight¶
目标
构建对应图后,目标是提取广义度信号的高频分量,然后对图中度发生快速变化的节点进行采样。
- 为了探索度信号频率和团之间的关系,本文研究了度信号对高通滤波器(拉普拉斯矩阵实现)的响应,应用于连通洞穴图,重点是度频率,这是一个完全由相邻节点确定的局部特征,其他类型的图可以简化为连通洞穴图。
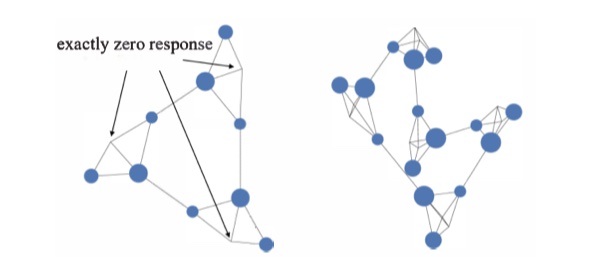
- 如下图所示,具有高响应的节点表现如下特性,将每个团视为一个社区:
- 在每个社区中,必须存在一个节点产生强烈的响应
- 在每个社区中有足够数量的节点可以引发强烈的响应
- 具有显著响应的节点位于每个社区的边缘,并且容易形成切点
- 它们不仅与其各自社区内的节点有联系,还与其他社区的节点有联系
- 上述特性促使对高频节点进行采样。最大团配准过程中包括搜索对应图中的所有最大团,为每个最大团生成假设并选择最佳团。假设输出样本由高频节点组成,那么:
- 由于这样的节点在每个社区中必须存在,它们可以覆盖几乎每个最大团
- 每个团中足够数量的样本可确保生成假设的能力
- 考虑节点之间的连接表示兼容性,所选的对应关系不仅与其所属团内的对应关系兼容,还与其他一些对应关系兼容,表明这些对应关系更可靠,从而生成更好的假设
- 在一个典型的图中,团要么相互连接要么不相互连接。相互连接的团保持着连通洞穴图的相似局部属性,而孤立的团表现出不同的特征。然而,孤立的团在配准中可以忽略不计。
Graph Filtering: Formulation¶
- 通过选择性地采样高频节点实现,有三种典型的图滤波器:高通、低通、全通滤波器
- 高通滤波器的简单设计是 Haar-like 的高通滤波器:
\[
\mathcal{H} = I - \mathcal{A} =V
\begin{bmatrix}
1- \lambda_1 & 0 & ... & 0 \\
0 & 1- \lambda_2 & ... & 0 \\
... & ... & ... & ... \\
0 & 0 & ... & 1- \lambda_N
\end{bmatrix}
V^{-1}
\]
- 低通滤波器是 Haar-like 的低通滤波器:
\[
\mathcal{H} = I + \frac{1}{|\lambda_{\text{max}}|}\mathcal{A} =V
\begin{bmatrix}
1 + \frac{\lambda_1}{|\lambda_{\text{max}}|} & 0 & ... & 0 \\
0 & 1 + \frac{\lambda_2}{|\lambda_{\text{max}}|} & ... & 0 \\
... & ... & ... & ... \\
0 & 0 & ... & 1 + \frac{\lambda_N}{|\lambda_{\text{max}}|}
\end{bmatrix}
V^{-1}
\]
- 全通滤波器,保留度信号的所有信息,并直观对度数较大的节点进行采样。
\[
\mathcal{H} = I
\]
- 对应图,对于对应图上的滤波器,首先计算广义度信号 \(s=[s_1, s_2, ..., s_N]^\top \in C^{N \times 1}, s_i = \sum_j W_{\text{SOG}_{\text{ij}}}\),然后用高通滤波器来过滤 \(s\) 的高频信息。定义高通滤波器为 \(\mathcal{H} = \text{Diag}(s) - W_{\text{SOG}}\) 或拉普拉斯矩阵。在图顶点域中,信号 \(X=(x_i), (\mathcal{H}X)_i = s_ix_i - \sum_{j \in \mathcal{N}_i} W_{\text{SOG}_{\text{ij}}} x_j\) 的输出反映了节点与其邻居组合之间的差异。然后得到 \(\mathcal{H}\) 对应的信号 \(s\) 的响应为 \(f = \mathcal{H}s\),它量化了经过高通图滤波后每个节点信号的能量,它反映了从图中的邻居中了解有关节点上信号值的信号量。
Stochastic Sampling¶
- 采样算子定义:在获得每个节点对图滤波器的响应幅度后,接着根据这个响应幅度进行采样。假设目标是从图信号 \(x = \mathcal{H}s \in C^n\) 的 \(m\) 个分量进行采样,以产生采样信号 \(y = x_{\mathcal{M}} \in C^m\)。采样算子和插值算子定义为线性映射。
- 非随机方法:尝试创建一个设计良好的确定性采样算子。
- 随机采样:采用一种随机策略。考虑从图滤波中获取的 \(\pi_i\) 作为采样分布,并在初始对应集上应用概率采样,从而产生一个表示为 \(C_{\text{sampled}} \cdot \pi_i\) 的采样集。近似于采样算子,它在最小化重构误差方面是最优的,并且速度更快。
 FastMAC: Stochastic Spectral Sampling of Correspondence Graph
FastMAC: Stochastic Spectral Sampling of Correspondence Graph