GeoTransformer¶

约 1822 个字预计阅读时间 6 分钟

Abstract

paper： Geometric Transformer for Fast and Robust Point Cloud Registration
code： GeoTransformer
Pre Knowledge
SuperPoint
KPConv

Idea¶

Introduction¶

一种 Geometric Transformer 的快速且鲁棒的点云配准方法
GeoTransformer 采用几何自注意力和特征交叉注意力模块，以学习点云的几何不变性
GeoTransformer 在建立全局与局部关系时采用超点匹配，并在超点匹配时使用了 overlap-aware circle loss，而不是传统的 Crossentropy 损失，这种方法可以避免交叉熵损失带来的高置信度匹配的抑制问题
GeoTransformer 是一种无需关键点检测和 RANSAC 的方法，能够提取准确的对应关系来进行点云配准

基于对应的方法 ¶

GeoTransformer 遵循基于对应的方法，依赖于显式的位置编码。近期的基于对应的方法中一般有两大类（GeoTransformer 是第二类）：

检测更多可重复的关键点并学习更鲁棒的关键点描述子
无需关键点检测，而是考虑所有可能的匹配

直接配准方法 ¶

直接匹配方法在单一合成形状中效果较好，但在大规模场景中会失败，原因是在于过分依赖全局特征，再复杂场景中更要兼容局部与全局性。直接配准方法一般有两大类：

ICP 思想，通过建立软分配关系，使用可微分加权的 SVD 计算变换（GeoTransformer 中点云匹配后也是用可微分加权的 SVD 来提取局部特征）
提取点云全局特征向量进行回归变换

深度鲁棒估计 ¶

GeoTransformer 提到在高离群值比情况下，RANSAC 方法收敛缓慢且不稳定，所以前人设计了一个深度鲁棒估计量，来摆脱异常值的干扰，而 GeoTransformer 使用了一个无参数的 LGR 算法（局部到全局配准方案），实现高效准确配准。

GeoTransformer Model¶

GeoTransformer 整体框架

GeoTransformer 的步骤分为特征提取、超点匹配、点云匹配和局部全局配准四个过程。

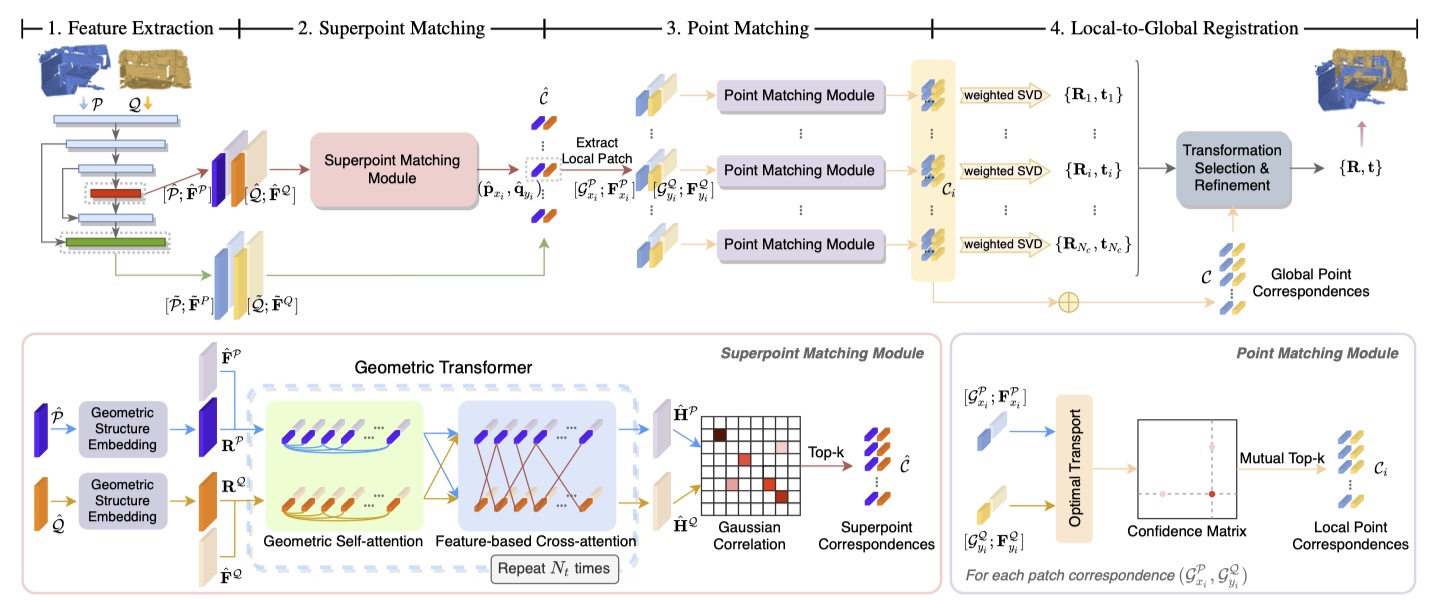
特征提取 ¶

特征提取利用 KPConv+FPN 的结构提取多层次特征，输入源点云和目标点云，输出 KPConv 的 output 的两个点云特征，以及输出 FPN 后的 output 的两个点云特征。

超点匹配 ¶

对于 KPConv 输出的点对关系输入到超点匹配模块，输出全局密集的点对应关系。超点匹配模块包括：几何自注意力模块，特征交叉注意力模块，计算高斯相关性，对应点采样。

几何自注意力模块 ¶

使用几何自注意力模块和特征交叉注意力模块的目的是学习不受变换影响且表达几何一致性的超点特征表示。

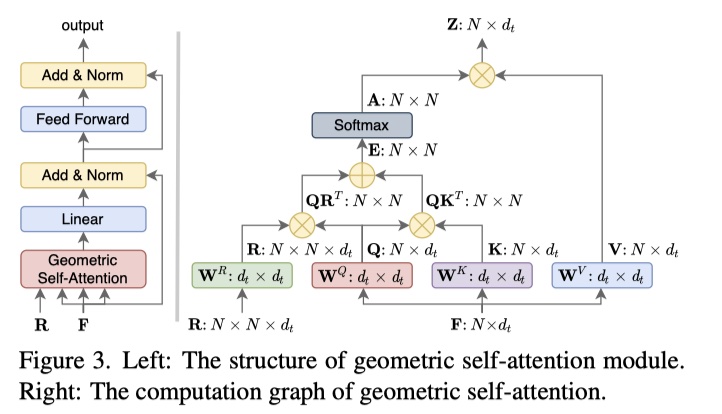
下图为几何自注意力模块（类似于结构自注意力机制），但是计算注意力得分公式并不相同：

\[e_{i,j}=\frac{(x_iW^Q)(x_jW^K+r_{i,j}W^R)^\top}{\sqrt{d_t}}\]

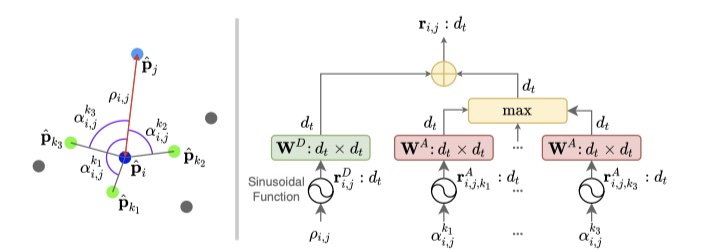
几何自注意力机制中更多考虑了几何关系，比如引入超点特征向量 \(x_i,x_j\)，几何结构嵌入向量 \(r_{i,j}\)，作为注意力机制中的 \(Q、K、R\) 的权重系数，通过几何关系来影响注意力机制。

\[r_{i,j} = r_{i,j}^DW^D + \max_x\{r_{i,j,x}^AW^A\}\]

特征交叉注意力模块 ¶

给定两个自注意力模块输出的特征矩阵，输入到交叉注意力机制，计算各自的特征矩阵 \(Z_i^Q,Z_i^P\)，并且计算注意力得分 \(e_{i,j}\)，公式如下：

\[ e_{i,j} = \frac{(x_i^PW^Q)(x_j^QW^K)^\top}{\sqrt{d_t}} \]

为什么要进行这两个注意力模块？

几何自注意力模块用于对点云变换不变几何结构进行编码，特征交叉注意力模块用于点云几何一致性进行建模，保证得到的混合特征对变换是不变的，不受变换影响。

计算高斯相关性 ¶

计算高斯相关性的目的是找互相重合的点云块（一块区域的点）。首先对超点特征向量归一化到单位超球面上，计算两个点云超点特征向量之间的高斯相关性得分，用来找到最相似的超点对，以得到高质量的超点对应关系（GeoTransformer 无需关键点匹配，所以只能优化匹配关系）。归一化公式如下：

\[ s_{i,j} = \exp(-\| \hat{h}_i^P - \hat{h}_j^Q \|_2^2) \]

另外为了避免有一些与多个点都高度匹配的点，抑制歧义匹配，还会进行双向归一化操作：

\[ \bar{s}_{i,j} = \frac{s_{i,j}}{\sum_{k=1}^{|\hat{Q}|}s_{i,k}} \cdot \frac{s_{i,j}}{\sum_{k=1}^{|\hat{P}|}s_{k,j}} \]

对应点采样 ¶

top-k 选择是用来对应点采样的一种方法，相较于随机采样，可以得到更确定性的点对应，用于后续的配准计算。

点匹配 ¶

对于上一环节已经找到相互重合的两个点云块，要继续找到里面的点云匹配对（化区域为个体）。
思路：计算一个点云块中一个点与另一个点云块中所有点的相似性，相似性最高的为匹配对
- 首先计算相似关系矩阵，并使用 Sinkhorn 算法设计分配矩阵 Z 来选择匹配对，为了使得整体匹配置信度达到最优，使用选择置信度最高的 K 个作为匹配对。

\[ \mathcal{C}_i =\{ (\mathcal{G}_{x_i}^P(x_j), \mathcal{G}_{y_i}^Q(y_j)) | (x_j, y_j) \in \mathrm{mutual\_topk}_{x, y}(z_{x, y}^i) \} \]

局部到全局的配准 ¶

在局部阶段，使用超点对应关系计算匹配矩阵后，根据上一步取匹配对后作为本轮结果，并将上一轮的匹配矩阵与本轮的匹配对进行比较，若不满意则去除，多次迭代，计算新的变换矩阵。

\[ R_i, t_i = \underset{R,t}{\min} \sum_{(\tilde{p}_{x_j}, \tilde{q}_{y_j}) \in C_i} w_j^i \| R \cdot \tilde{p}_{x_j} + t - \tilde{q}_{y_j} \|_2^2 \\ R, t = \underset{R_i,t_i}{\max} \sum_{(\tilde{p}_{x_j}, \tilde{q}_{y_j}) \in C} \left [ \| R_i \cdot \tilde{p}_{x_j} + t_i - \tilde{q}_{y_j} \|_2^2 < \tau_a \right ] \]

Loss¶

计算局部点对应关系损失 \(L_{oc}\)(overlap-aware circle loss) 和全局点对损失 \(L_p\) 两部分相加
- \(L_{oc}\) 关注点对间的重叠关系，给重叠较高的点对以更大权重，同时关注正负样本的重叠
- \(L_p\) 采用负对数似然损失，对稀疏的全局点对关系进行监督，分别考虑点对关系和两个点云的内部点间的关系

\[ \mathcal{L}_{oc}^P = \frac{1}{|\mathcal{A}|} \sum_{\mathcal{G}_i^P \in \mathcal{A}} \log [1 + \sum_{\mathcal{G}_j^Q \in \epsilon_p^i} e^{\lambda_i^j \beta_p^{i, j}(d_i^j - \Delta_p)} \cdot \sum_{\mathcal{G}_k^Q \in \epsilon_n^i} e^{\beta_n^{i,k} (\Delta_n - d_i^k)}] \\ \mathcal{L}_{p, i} = -\sum_{(x,y) \in \mathcal{M}_i} \log{\bar{z}_{x,y}^i} - \sum_{x \in \mathcal{I}_i} \log{\bar{z}_{x, m_i + 1}^i} - \sum_{y \in \mathcal{J}_i} \log{\bar{z}_{n_i + 1, y}^i} \]

Experiment¶

Reference¶

最后更新: 2025年2月18日 10:23:48
创建日期: 2025年2月18日 10:23:48