RNNs¶

概述 ¶

全连接神经网络 DNN 和 卷积神经网络 CNN，它们的前一个输入和后一个输入是没有关系的。当我们处理序列信息时，某些前面的输入和后面的输入是有关系的，比如：当我们在理解一句话的意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；这个时候我们就需要使用到循环神经网络（Recurrent Neural Network）。

RNN 在自然语言处理领域最先被使用起来，RNN 可以为语言模型进行建模：

我没有完成上级布置给我的任务，所以 被开除了

让电脑来填写下划线的词最有可能的是『我』，而不太可能是『小明』，甚至是『吃饭』。

语言模型就是这样的东西：给定一个一句话前面的部分，预测接下来最有可能的一个词是什么。

基本循环神经网络 ¶

基本的 RNN，结构由输入层、一个隐藏层和输出层组成。

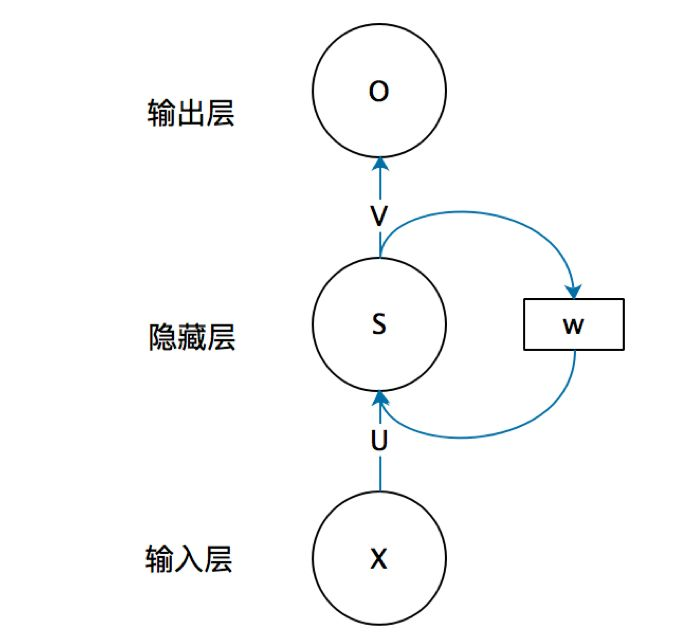
• x 是输入向量
• o 是输出向量
• s 表示隐藏层的值
• U 是输入层到隐藏层的权重矩阵
• V 时隐藏层到输出层的权重矩阵

循环神经网络的隐藏层的值 s 不仅仅取决于当前这次的输入 x，还取决于上一次隐藏层的值 s。权重矩阵 W 就是隐藏层上一次的值作为这一次的输入的权重。

将上图的基本 RNN 结构在时间维度展开（RNN 是一个链式结构，每个时间片使用的都是相同的参数）

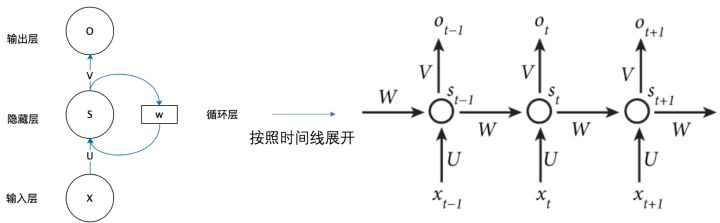
这个网络在 t 时刻接收到输入 \(x_t\) 之后，隐藏层的值是 \(s_t\)，输出层的值是 \(o_t\)，关键的是，\(s_t\) 的值不仅仅取决于 \(x_t\)，还取决于 \(s_{t-1}\)。

• 公式 1 是隐藏层的计算公式，它是循环层。U 是输入 x 的权重矩阵，W 是 上一次隐藏层值 \(s_{t-1}\) 作为则一次的输入的权重矩阵，f 是激活函数。
• 公式 2 是输出层的计算公式，V 是输出层的权重矩阵，g 是激活函数。
• 隐藏层有两个输入，第一是 U 与 \(x_t\) 向量的乘积，第二是上一隐藏层输出的状态 \(s_{t-1}\) 与 W 的乘积。等于上一个时刻计算的 \(s_{t-1}\) 需要缓存一下，在本次输入 \(x_t\) 一起计算，共同输出最后的 \(o_t\)。

如果反复把公式 1 带入公式 2，可以得到：

从上面可以看出，循环神经网络的输出值，是受前面历次输入值 \(x_t、x_{t-1}、x_{t-2}、x_{t-3}、...\) 影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。这样其实不好，因为如果太前面的值和后面的值已经没有关系了，循环神经网络还考虑前面的值的话，就会影响后面值的判断。

双向循环神经网络 ¶

对于语言模型来说，很多时候光看前面的词是不够的，比如下面这句话：我的手机坏了，我打算 一部新的手机。 我们这个时候就需要双向循环神经网络。

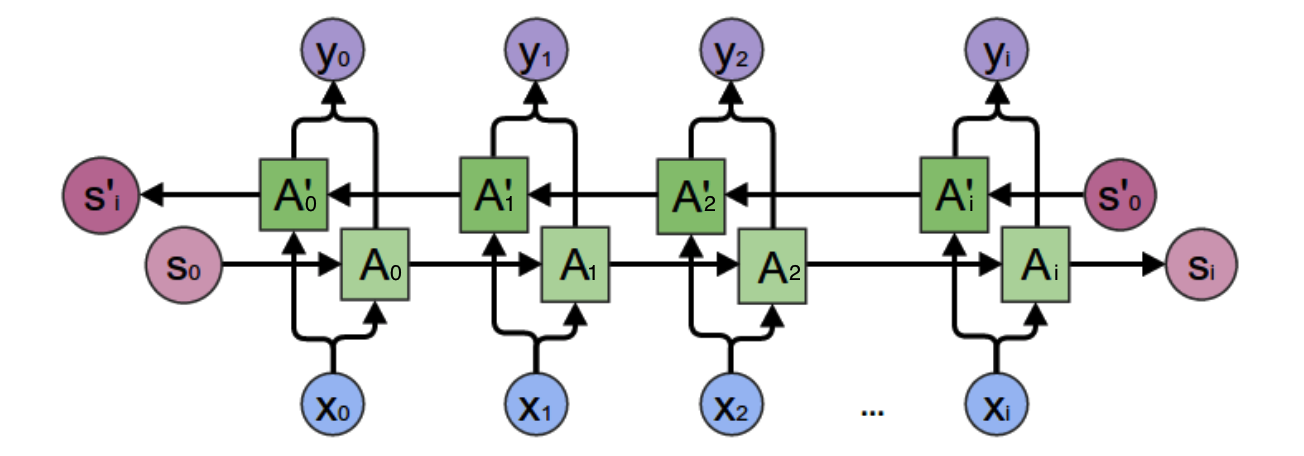
从上图可以看出，双向循环神经网络的隐藏层需要保存两个值，一个 \(A\) 参与正向计算，另一个值 \(A^\prime\) 参与反向计算。最终的输出值 \(y_2\) 取决于 \(A_2\) 和 \(A_2^\prime\)。其计算方法为：

\(A_2\) 和 \(A_2^\prime\) 的计算方法为：

现在可以看出一般的规律：正向计算时，隐藏层的值 \(S_t\) 与 \(S_{t-1}\) 有关；反向计算时，隐藏层的值 \(S_t^\prime\) 与 \(S_{t+1}^\prime\) 有关；最终的输出取决于正向和反向计算的加和。现在，仿照公式 1 和公式 2，写出 BRNN 的计算公式：

从上面三个公式可以看到，正向计算和反向计算不共享权重，也就是说 \(U\) 和 \(U^\prime\)、\(W\) 和 \(W^\prime\)、\(V\) 和 \(V^\prime\) 是不同的权重矩阵。

梯度爆炸和梯度消失 ¶

上文介绍的几种 RNN 并不能很好地处理较长的序列，RNN 在训练中很容易发生梯度爆炸和梯度消失，这导致梯度不能在较长序列中一直传递下去，从而使 RNN 无法捕捉到长距离的影响。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会收到 NaN 错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

1、合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域。

2、使用 relu 代替 sigmoid 和 tanh 作为激活函数。

3、使用其他结构的 RNNs，比如长短时记忆网络（LTSM）和 Gated Recurrent Unit（GRU），这是最流行的做法。

长短期记忆网络 LSTM ¶

原始 RNN 的隐藏层只有一个状态，即 h，它对短期的输入非常敏感。那么如果我们再加一个门（gate）机制用于控制特征的流通和损失，即 c，让它来保存长期的状态，这就是长短时记忆网络（Long Short Term Memory，LSTM）。

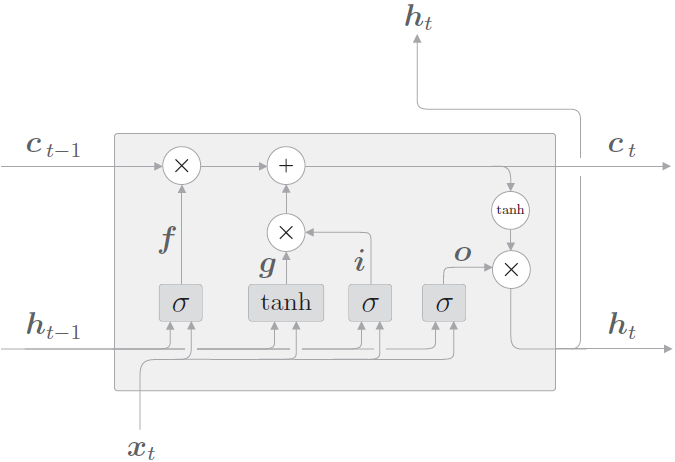
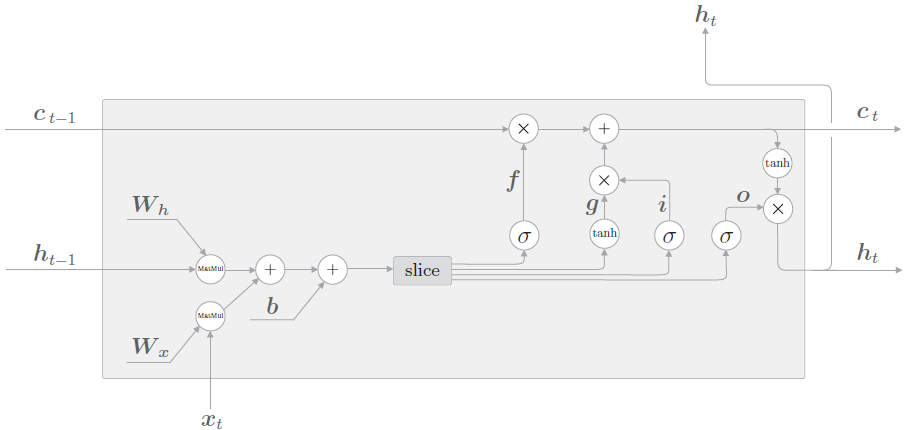
新增加的状态 c，称为单元状态。把 LSTM 按照时间维度展开：

可以看到在 t 时刻

• LSTM 的输入有三个：当前时刻网络的输入值 \(x_t\)、上一时刻 LSTM 的输出值 \(h_{t-1}\)、以及上一时刻的记忆单元向量 \(c_{t-1}\)。
• LSTM 的输出有两个：当前时刻的 LSTM 输出值 \(h_t\)、和当前时刻的记忆单元向量 \(c_t\)。

记忆单元 c 在 LSTM 层内部结束工作，不向其他层输出。LSTM 的输出仅有隐藏状态向量 h。

LSTM 的关键是单元状态，即贯穿图表顶部的水平线，有点像传送带。这一部分一般叫做单元状态（cell state），它自始至终存在于 LSTM 的整个链式系统中。

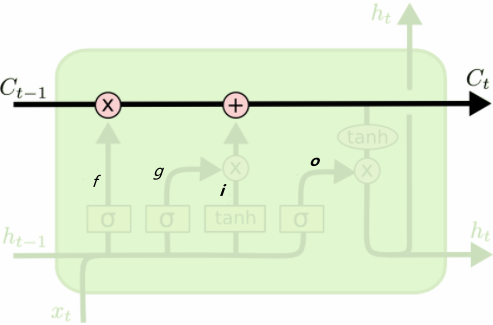
记忆单元状态的计算公式：\(公式1：c_{t}=f_{t} \odot c_{t-1}+i_{t} \odot g_t\)

遗忘门 ¶

\(f_t\) 叫做遗忘门，表示 \(C_{t-1}\) 的哪些特征被用于计算 \(C_t\)。\(f_t\) 是一个向量，向量的每个元素均位于 (0~1) 范围内。通常我们使用 sigmoid 作为激活函数，sigmoid 的输出是一个介于 (0~1) 区间内的值，但是当你观察一个训练好的 LSTM 时，你会发现门的值绝大多数都非常接近 0 或 1，其余的值少之又少。

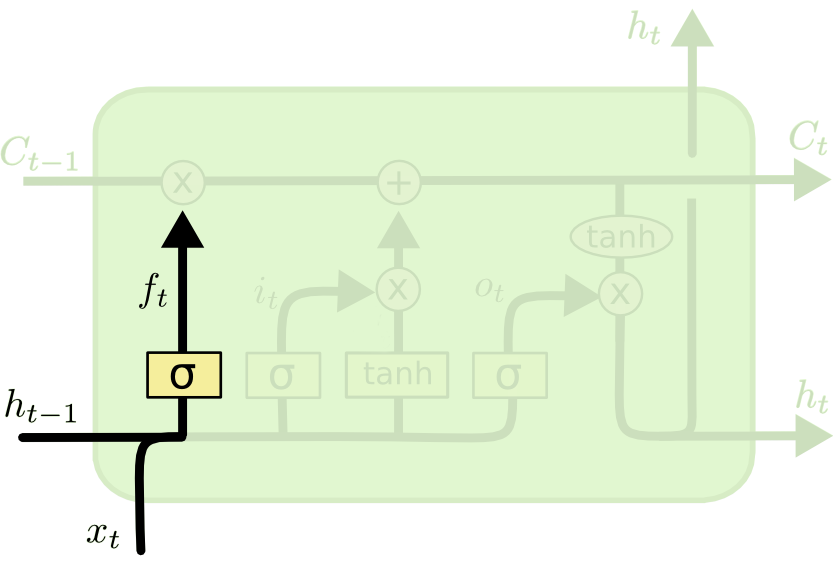
遗忘门的计算公式：\(公式2：f_t=\sigma (x_tW_x^{(f)}+h_{h-1}W_h^{(f)}+b^{(f)})\)

输入门 ¶

\(\tilde{C}_t\) 表示单元状态更新值，有输入数据 \(x_t\) 和隐节点 \(h_{t-1}\) 经由一个神经网络层得到，单元状态更新值的激活函数通常使用 tanh。\(i_t\) 叫做输入门，同 \(f_t\) 一样也是一个元素介于 (0~1) 区间内的向量，同样由 \(x_t\) 和 \(h_{t-1}\) 经由 sigmoid 激活函数计算而成。

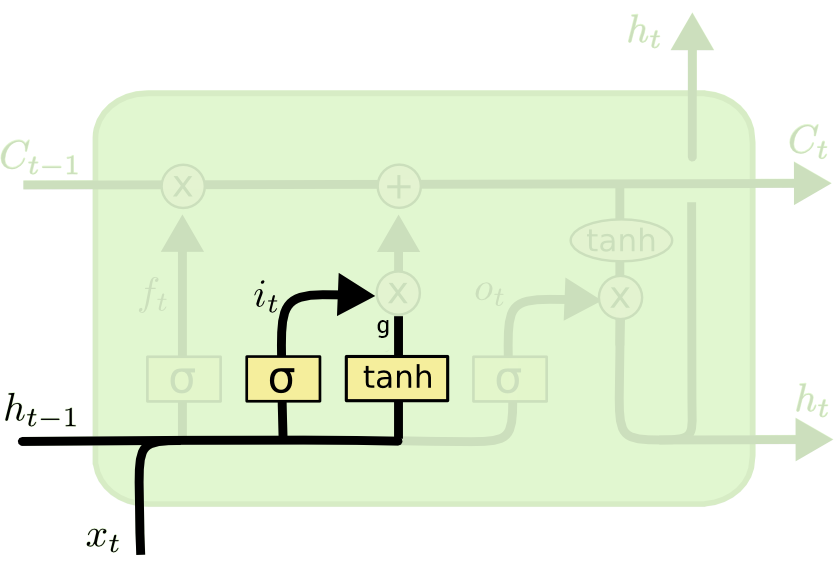
输入门和单元更新值的计算方式：

• \(公式3：i_t=\sigma (x_tW_x^{(i)}+h_{t-1}W_h^{i}+b^{(i)})\)
• \(公式4：g_t=tanh(x_tW_x^{(g)}+h_{t-1}W_h^{(g)}+b^{(g)})\)

输出门 ¶

最后，为了计算预测值 \(\hat{y}_t\) 和生成下个时间片完整的输入，我们需要计算隐节点的输出 \(h_t\)。

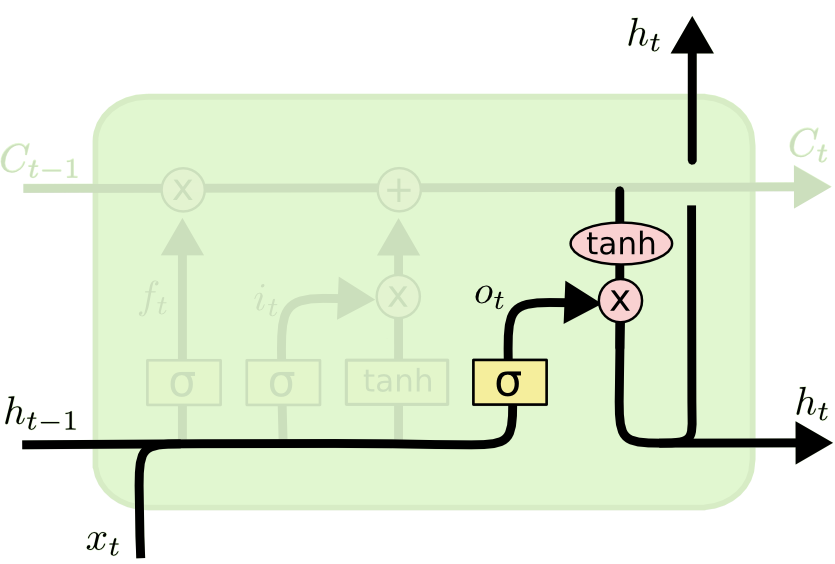
输出门和隐节点的计算公式

• \(公式5：o_t=\sigma (x_tW_x^{(o)}+h_{t-1}W_h^{(o)}+b^{(o)})\)
• \(公式6：h_t=o_t\odot tanh(c_t)\)

我们来看公式 2、3、4、5，都是型如 \(xW_x+hW_h+b\) 的格式，因此可以整合为通过一个式子进行，如下图所示：

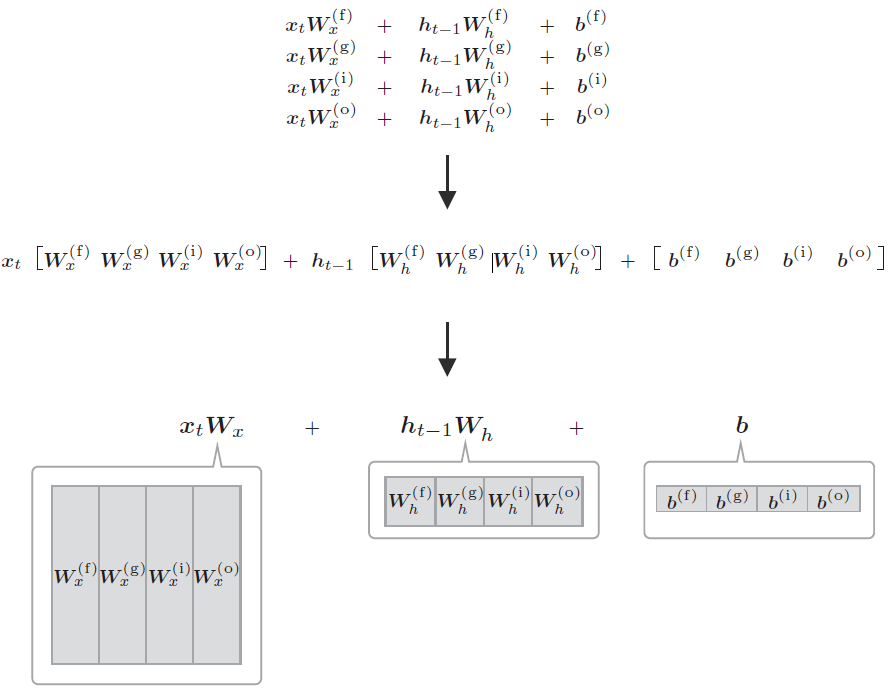
4 个权重（或偏置）被整合为了 1 个。如此，原本单独执行 4 次的仿射变换通过 1 次计算即可完成，可以加快计算速度。这是因为矩阵库计算“大矩阵”时通常会更快，而且通过将权重整合到一起管理，源代码也会更简洁。

假设 \(W_x、W_h\) 和 \(b\) 分别包含 4 个权重（或偏置），此时 LSTM 的计算图如下所示。

import tensorflow as tf
from tensorflow.keras import layers

inputs = tf.random.normal((64, 6, 10))
LSTM_layer = layers.LSTM(units=20, return_sequences=True, return_state=True)
outputs, final_memory_state, final_carry_state = LSTM_layer(inputs)
print(outputs.shape, final_memory_state.shape, final_carry_state.shape)
# (64, 6, 20) (64, 20) (64, 20)

print(len(LSTM_layer.weights))  # 3
print(LSTM_layer.weights[0].shape)  # Wx (10, 80)
print(LSTM_layer.weights[1].shape)  # Wh (20, 80)
print(LSTM_layer.weights[2].shape)  # bias (80,)

门控循环单元 GRU ¶

LSTM 的参数太多，计算需要很长时间。因此，最近业界又提出了 GRU（Gated RecurrentUnit，门控循环单元）。GRU 保留了 LSTM 使用门的理念，但是减少了参数，缩短了计算时间。

相对于 LSTM 使用隐藏状态和记忆单元两条线，GRU 只使用隐藏状态。异同点如下：

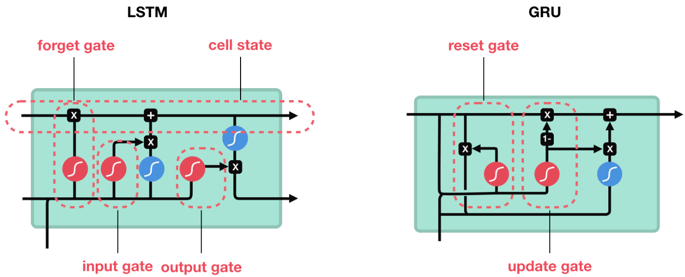
GRU 的计算图如下所示。

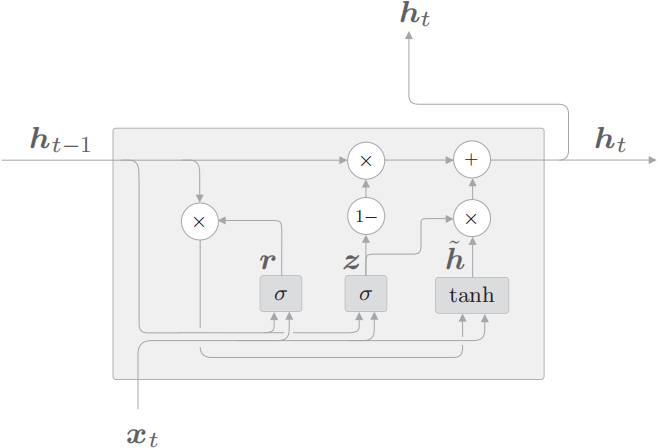
GRU 计算图中，\(\sigma\) 节点和 tanh 节点有专用的权重，节点内部进行仿射变换（“1−”节点输入 x，输出 1 − x）

\(公式2.1：z=\sigma(x_t W_x^{(z)}+h_{t-1} W_h^{(z)}+b^{(z)})\)

\(公式2.2：r=\sigma(x_t W_x^{(r)}+h_{t-1} W_h^{(r)}+b^{(r)})\)

\(公式2.3：\tilde{h}=\tanh (x_t W_x+(r \odot h_{t-1}) W_h+b)\)

\(公式2.4：h_t=(1-z) \odot h_{t-1}+z \odot \tilde{h}\)

GRU 中进行的计算由上述 4 个式子表示（这里 \(x_t\) 和 \(h_{t−1}\) 都是行向量），如图所示，GRU 没有记忆单元，只有一个隐藏状态 h 在时间方向上传播。这里使用 r 和 z 共两个门（LSTM 使用 3 个门），r 称为 reset 门，z 称为 update 门。

• r（reset 门） 决定在多大程度上“忽略”过去的隐藏状态。根据公式 2.3，如果 r 是 0，则新的隐藏状态 \(\tilde{h}\) 仅取决于输入 \(x_t\)。也就是说，此时过去的隐藏状态将完全被忽略。
• z（update 门） 是更新隐藏状态的门，它扮演了 LSTM 的 forget 门和 input 门两个角色。公式 2.4 的 \((1-z) \odot h_{t-1}\) 部分充当 forget 门的功能，从过去的隐藏状态中删除应该被遗忘的信息。\(z \odot \tilde{h}\) 的部分充当 input 门的功能，对新增的信息进行加权。