神经网络与深度学习 ¶
约 1188 个字 7 张图片 预计阅读时间 4 分钟
Abstract
学习自 邱锡鹏老师 的神经网络与深度学习,归档一些学习笔记。
概述 ¶
神经网络与深度学习是人工智能的一个子领域
- 神经网络:一种以(人工)神经元为基本单元的模型
- 深度学习:一类机器学习问题,主要解决贡献度分配问题。
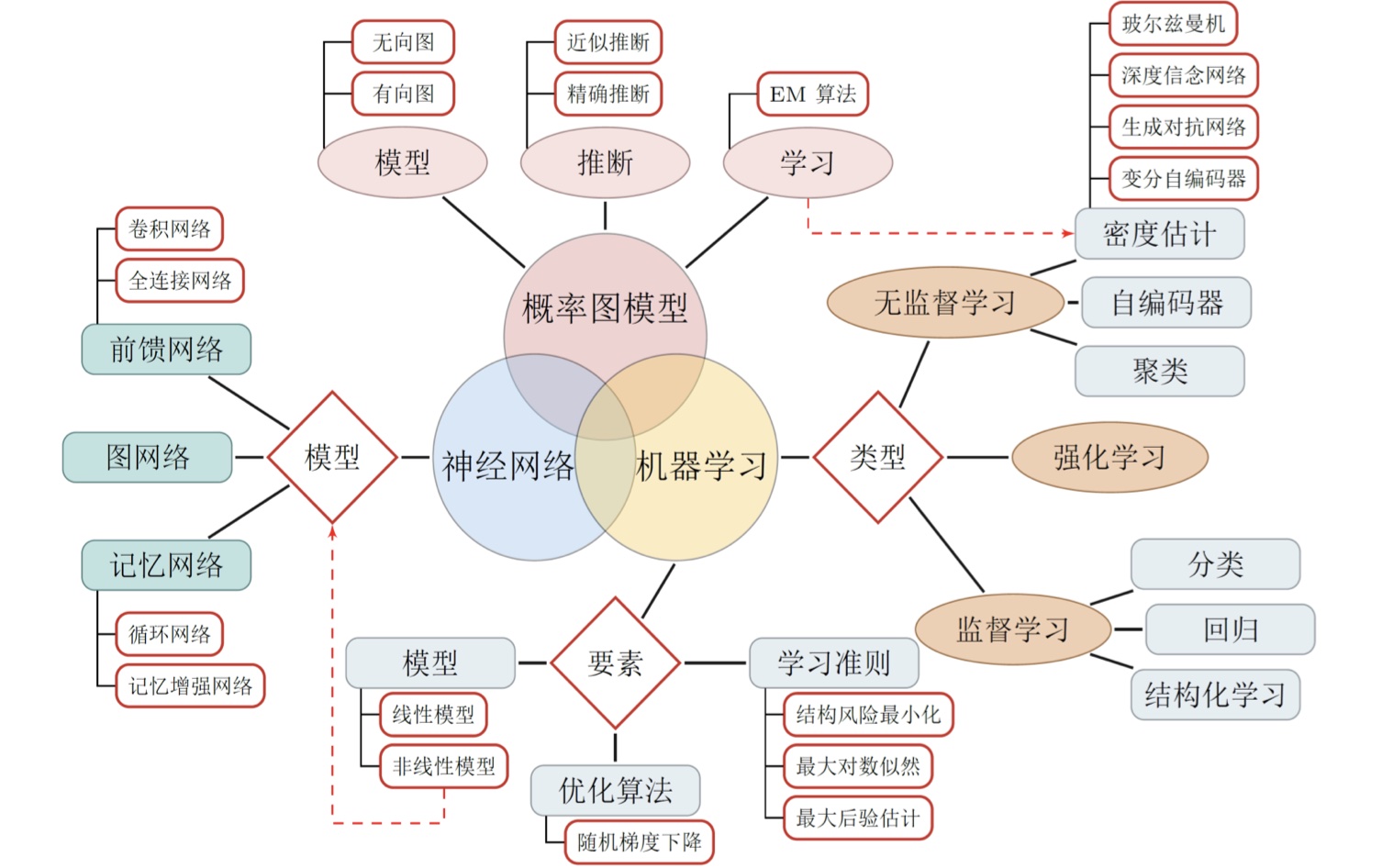
人工神经网络 ¶
- 人工神经网络主要由大量的神经元以及它们之间的有向连接构成。因此考虑三方面
- 神经元的激活规则:主要是指神经元输入到输出之间的映射关系,一般为非线性函数
- 网络的拓扑结构:不同神经元之间的链接关系
- 学习算法:通过训练数据来学习神经网络的参数
- 人工神经网络由神经元模型构成,这种由许多神经元组成的信息处理网络具有并行分布结构
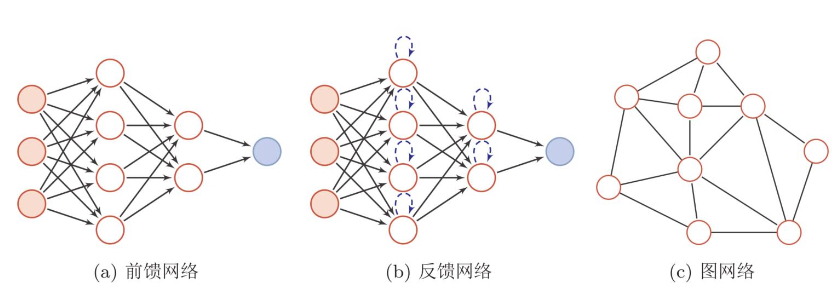
前馈神经网络 ¶
网络结构 ¶
- 在前馈神经网络中,各神经元分别属于不同的层。整个网络中无反馈,信号从输入层向输出层单向传播,可用一个有向无环图表示
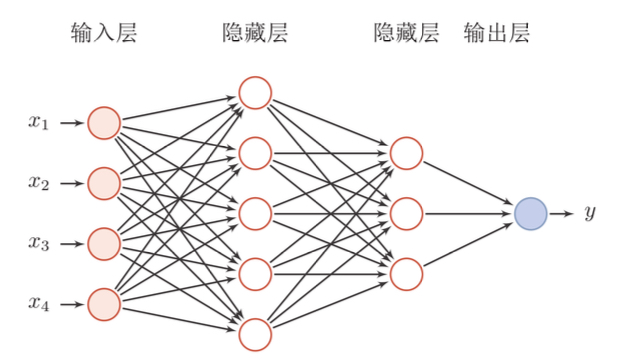
通用近似定理 ¶
- 对于具有线性输出层和至少一个使用”挤压“性质的激活函数的隐藏层组成的前馈神经网络。只要其隐藏层神经元的数量足够,它可以以任意精度来近似任何从一个定义在实数空间中的有界闭集函数
应用到机器学习 ¶
- 模型:\(y=f^5(f^4(f^3(f^2(f^1(x)))))\)
- 学习准则:\(L(y,y^*)\)
- 优化(梯度下降
) :\(\frac{\partial L(y,y^*)}{\partial f^1} = \frac{\partial f^2}{\partial f^1} \times \frac{\partial f^3}{\partial f^2} \times \frac{\partial f^4}{\partial f^3} \times \frac{\partial f^5}{\partial f^4} \times \frac{\partial L(y,y^*)}{\partial f^5}\)
计算图与自动微分 ¶
- 复合函数 \(f(x;w,b)=\sigma(wx+b)\) 的计算图
- 链式法则:\(\frac{\partial f(x;w,b)}{\partial w}=\frac{\partial f(x;w,b)}{\partial h_6} \frac{\partial h_6}{\partial h_5} \frac{\partial h_5}{\partial h_4} \frac{\partial h_4}{\partial h_3} \frac{\partial h_3}{\partial h_2} \frac{\partial h_2}{\partial h_1} \frac{\partial h_1}{\partial w}\)
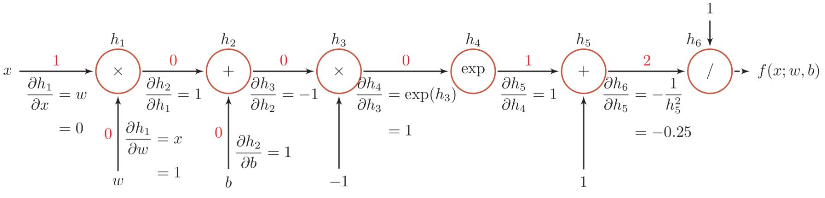
- 反向传播算法只是自动微分的一种特殊形式
优化问题 ¶
- 非凸优化问题:\(y=\sigma(w \ 2 \ \sigma(w \ 1 \ x))\) 的损失函数
- 梯度消失问题:在每一层都要乘以该层的激活函数的导数
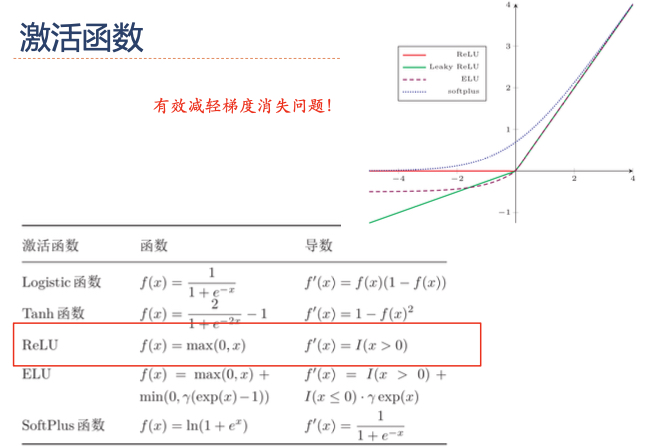
激活函数 ¶
- 有效减轻梯度消失问题
卷积神经网络 ¶
卷积 ¶
- 卷积经常用在信号处理中,用于计算信号的延迟累积
- 假设一个信号发生器每个时刻 t 产生一个信号 \(x_t\),其信号的衰减率为 \(w_k\),即在 k-1 个时间步长后,信息为原来的 \(w_k\) 倍,假设 \(w_1=1,w_2=1/2,w_3=1/4\)
- 时刻 t 收到的信号 \(y_t\) 为当前时刻产生的信息和以前时刻延迟信息的叠加
- 即 \(y_t=w_1 \times x_t+w_2 \times x_{t-1}+w_3 \times x_{t-2}=\sum_{k=1}^3w_k \cdot x_{t-k+1}\),\(y_t\) 称为滤波器或卷积核
一维卷积 ¶
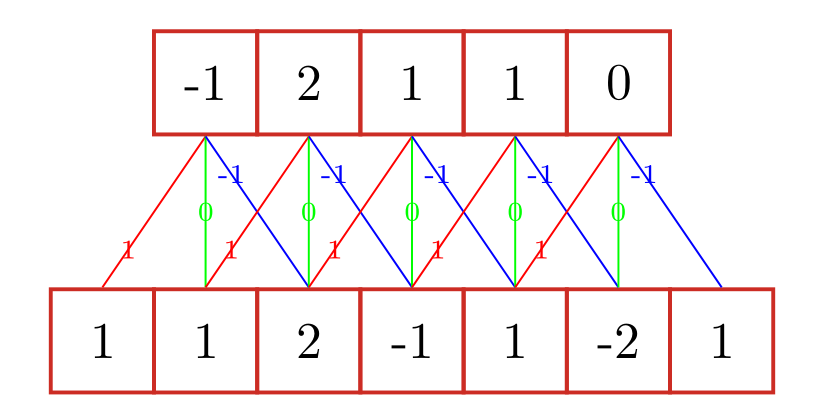
二位卷积 ¶
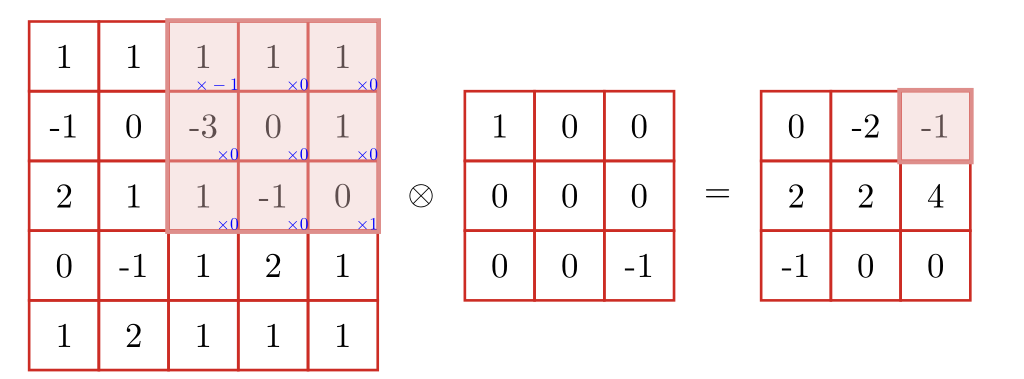
作用 ¶
- 卷积作为特征提取器
- 卷积代替全连接
- 可以引入多组滤波器
- 卷积层
- 典型的卷积层为 3 维结构
- 汇聚层
- 卷积层虽然可以显著减少连接的个数,但是每一个特征映射的神经元个数并没有显著减少
卷积网络结构 ¶
- 卷积网络是由卷积层、子采样层、全连接层交叉堆叠而成
- 趋向于小卷积、大深度
- 趋向于全卷积
- 一个卷积块为连续个 M 个卷积层和 b 个汇聚层(M 通常设置为 2-5,b 为 0 或 1
) 。一个卷积网络中可以堆叠 N 个连续的卷积块,然后在接着 K 个全连接层(N 的取值区间比较大,比如 1-100 或者更大;K 一般为 0-2)
转置卷积 / 微步卷积 ¶
- 低维特征映射到高维特征
空洞卷积 ¶
- 如何增加输出单位的感受野
- 增加卷积核的大小
- 增加层数来实现
- 在卷积之前进行汇聚操作
- 空洞卷积通过给卷积核插入“空洞”来变相地增加其大小
简单的残差单元结构 ¶
\[
h(\mathbf{x})=\mathbf{x}+(h(\mathbf{x})-\mathbf{x}) \\
\mathbf{x} 为恒等函数,h(\mathbf{x})-\mathbf{x} 为残差函数 f(\mathbf{x}, \theta)
\]
应用 ¶
- AlphaGo
- Mask RCNN
- 图像生成
- Deep Dream
- 画风迁移
- 对抗样本