机器学习 ¶

概述 ¶

概念 ¶

机器学习的目标是从原始数据中提取特征，学习一个映射函数 \(f\) 将上述特征（或原始数据）映射到语义空间，寻找数据和任务目标之间的关系。

即 机器学习 \(\approx\) 构建一个映射函数

种类 ¶

监督学习 ¶

• 给定带有标签信息的训练集合，学习从输入到输出的映射
• 一般被应用在回归或分类的任务中
• 在训练过程中希望映射函数在训练数据集上得到所有样本的“损失和”最小
• 损失函数包括 0-1 损失函数（相等为 0，反之为 1），平方损失函数，绝对 - 损失函数，对数损失函数（对数似然函数）
• 监督学习一般包含三个部分内容：
  • 从训练数据集中学习得到映射函数 f
  • 在测试数据集上测试映射函数 f
  • 在未知数据集上测试映射函数 f（投入使用）
• 训练及中产生的损失一般称为经验风险（empirical risk），越小对训练集拟合效果越好
• 测试集中加入从真实数据分布采样的样本时，测试集上的损失会不断逼近期望风险（expected risk），越小模型越好
• 机器学习的目标是追求期望风险最小化
• 结构风险最小化（structural risk minimization）：防止过学习，基于过学习时参数值通常都较大这一发现，在经验风险上加上表示模型复杂度的正则化项（regularizer）或惩罚项（penalty term），在最小化经验风险与降低模型复杂度之间寻找平衡
• 主要的监督学习方法：
  • 判别方法（discriminative approach）
    • 直接学习判别函数 f(X) 或者条件概率分布 P(Y|X) 作为预测的模型
    • 典型判别模型包括回归模型、神经网络、支持向量机和 Ada boosting
  • 生成方法（generative approach）
    • 从数据中学习联合概率分布 P(X, Y)（通过似然概率 P(X|Y) 和类概率 P(Y) 乘积来求）
    • 生成模型典型方法为贝叶斯方法、隐马尔可夫链
    • 难点在于联合分布概率或似然概率很难求

无监督学习 ¶

• 最大特点是数据无标签
• 一般被应用在聚类或若干降维任务中
• 半监督学习依赖于部分被标注的数据

强化学习 ¶

一种序列数据决策学习方法 从与环境交互中学习，通过回报值（reward）让智能体（agent）学习到在不同状态（state）下如何选择行为方式（action）

多元线性回归 ¶

• 有 \(n\) 个特征 \([x_1, ..., x_n]^{\top}\)，\(m\) 个训练数 \(\{(\mathbf{x_i}, \mathbf{y_i})\}_{i=1}^m\)，需要找到参数 \(\mathbf{\theta}\) 使得线性函数 \(h_\theta(\mathbf{x})=\theta_0+\mathbf{\theta}^{\top} \mathbf{x}\) 最小化均方误差函数

矩阵求逆 ¶

对均方误差函数求导得 \(\nabla J(\mathbf{\theta})=-\frac{1}{m}\mathbf{X}(\mathbf{y} - \mathbf{X}^{\top} \mathbf{\theta})\)，令梯度等于 0 得

梯度下降 ¶

\(x_j^{(i)}\) 表示第 \(i\) 个样本中第 \(j\) 个特征。

特征归一化 ¶

使得所有不同的特征尺度近似。

常用方法：均值归一化 : \(x_i=\frac{x_i - \mu_i}{x_{i\_max}-x_{i\_min}}\)

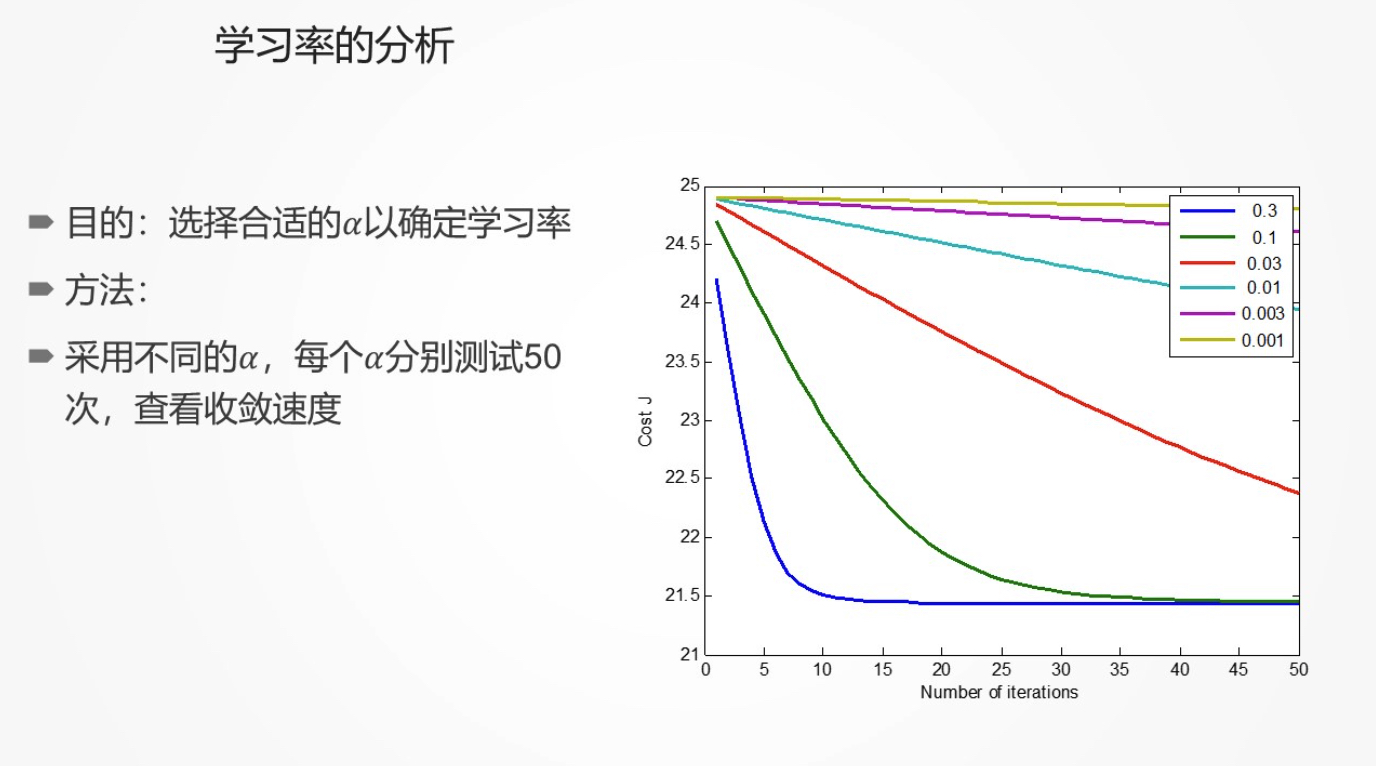
学习率 ¶

建议选择策略：...,0.001,0.003,0.01,0.03,0.1,0.3,... 通过代价收敛图，分析选择合适的 \(\alpha\)

对比 ¶

• 梯度下降
  • 需要确定 \(\alpha\)
  • 需要多次循环
  • 特征数 \(n\) 很大时也可以很好工作
  • 特征需要归一化
• 矩阵求逆
  • 不需要选择 \(\alpha\)
  • 不需要循环
  • 要计算 \((X^{\top} X)^{-1}\)
  • 如果特征数 \(n\) 很大，算法会非常慢，对内存要求高
  • 特征不需要归一化

实验报告 ¶

机器学习 -- 线性回归

724 KB / 12 P / 2023-09-23

下载

逻辑回归 ¶

• 线性回归对离群点非常敏感，导致模型不稳定，为了缓解这个问题可以考虑逻辑斯蒂回归（logistic regression）

分类 ¶

• 逻辑回归是分类模型，不是回归模型
• 二分类问题：\(y \in \{0, 1\}\)，0 表示负样本，1 表示正样本
• \(h_\theta(x)\) 可能 \(>1\) 或 \(<0\)，逻辑回归的目的：\(0 \le h_\theta(x) \le 1\)

学习模型 ¶

• 逻辑回归的模型：\(h_\theta(x)=g(\theta^{\top}x)\)，其中 \(g(z)=\frac{1}{1+e^{-z}}\)，称为逻辑函数（logistic function）或 Sigmoid 函数

• 逻辑回归代价函数
  • 满足分类的目的
  • 保证收敛（凸函数）

简化的代价函数及梯度下降 ¶

• 逻辑回归代价函数：

  \[ J(\theta)=\frac{1}{m} \sum_{i=1}^m Cost(h_\theta(x^{(i)}),y^{(i)}) \\ =-\frac{1}{m} \sum_{i=1}^m [y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))] \]
  • 优化模型：\(\underset{\theta}{\min} J(\theta)\)
  • 要给定的样本 \(\mathbf{x}\)，预测 \(y\)，输出 \(h_\theta(x)=\frac{1}{1+e^{-\theta \top x}}\)

• 梯度下降

  \[ \frac{\partial J(\theta)}{\partial x}= \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \]
  • 目标：\(\underset{\theta}{\min} J(\theta)\)
  • 区别：线性回归：\(h_\theta (x)=\theta^\top X\)，逻辑回归：\(h_\theta(x)=\frac{1}{1-e^{- \theta \top X}}\)

高级优化问题 ¶

优化算法 ¶

• cvxpy 系列，cvxpy，cvxOPT，这几个包主要解决凸优化问题
• scipy.optimizes.scipy 也有优化方法

scipy.optimize¶

• 使用各种算法（例如 BFGS，Nelder-Mead simplex，Newton Conjugate Gradient，COBYLA 或 SLSQP）对多变量标量函数（最小化（））进行无约束和约束最小化
• 全局（强力）优化程序（例如，退火（），流域购物（））
• 最小二乘最小化（leastsq（））和曲线拟合（curve_fit（））算法
• 标量但变量函数最小化器（minimize_scalar（））和根查找器（newton（））
• 使用各种算法的多变量方程系统求解器（root（））（例如混合 Powell，Levenberg-Marquardt 或大规模方法，如 Newton-Krylov）

多分类问题 ¶

• 一 VS 多 \(\to\) 1 VS 其他 转换为 一 VS 多 \(\to\) 1 VS 另一类
• 构建分类器
• 树状分类器构建，聚类 + 决策树来搜索类别差距
• 解决方法：
  • 训练：为每个类别 i，训练一个分类器 \(h_\theta^{(i)}(x)\)，以预测 \(y=i\) 的概率
  • 测试：给定一个测试样本 x，测试每个类别模型 \(h_\theta^{(i)}(x)\)，选择满足 \(\underset{i}{\max} h_\theta^{(i)}(x)\) 的 i，即为最优类别

实验报告 ¶

机器学习 -- 逻辑回归

938 KB / 9 P / 2023-10-10

下载

数据可视化 ¶

• matplotlib
• seaborn
• pyecharts
• Pandas

支持向量机 ¶

• 支持向量机 SVM 是一类按监督学习方式对数据进行二元分类的广义线性分类器
• 决策边界是对学习样本求解的最大边距超平面
• 解决线性可分问题
• 将线性可分问题中得到的结论推广到线性不可分——核函数

线性可分 VS 线性不可分 ¶

线性可分 ¶

• 二维：一条直线
• 三维：一个平面
• 四维及更高维：一个超平面 Hyperplane
• 数学定义：一个训练样本集 \(\{(X_1,y_1),(X_2,y_2),...,(X_n,y_n)\}\)，在 \(i=1 \sim N\) 线性可分，是指存在 \((\omega_1,\omega_2,b)\)，使得对 \(i=1 \sim N\)，有
  • 若 \(y_i =+1\)，则 \(\omega_1 x_{i1} + \omega_2 x_{i2} + b > 0\)
  • 若 \(y_i =-1\)，则 \(\omega_1 x_{i1} + \omega_2 x_{i2} + b < 0\)

• 支持向量机超平面与最优化

  • 假定样本集线性可分
  • SVM 要寻找的就是具有最大 margin 的超平面，且离两边的支持向量距离相等，可表示为
  \[ \min \frac{1}{2} \parallel \omega \parallel^2 \\ 约束条件：y_i(\omega^\top X_i + b) \ge 1 \ \ \ (i=1 \sim N) \]

线性不可分 ¶

• 如果 \(y_i=\{+1,-1\}\)，一个训练样本集 \(\{(X_i,y_i)\}\)，在 \(i=1 \sim N\) 线性可分，是指存在 \((\omega, b)\)，使得对 \(i=1 \sim N\)，有 \(y_i(\omega^\top X_i + b) > 0\)
• 典型的线性不可分问题——异或
• 非线性决策边界
  • 需要一个高阶模型以实现这样的非线性分类问题，本质是将二维空间问题映射为高维空间问题
  • 低维到高维的映射——核函数（理论上几乎通用于所有分类
• Cover 定理
  • 在一个 M 维空间上随机取 N 个训练样本随机的对每个训练 d 赋予标签 +1 或 -1
  • 这些训练样本线性可分的概率为 \(P(M)\)，则当 M 趋向无穷大时 \(P(M)=1\)
  • M 上升 \(\to\) \((\omega, b)\) 维度上升 \(\to\) 模型自由度上升 \(\to\) 线性可分概率上升
• 如何寻找核函数

核函数 ¶

• 线性核函数 \(K(x,xi)=x \cdot xi\)
• 多项式核 Polynomial kernel \((x^\top l+常量)^{常量}\)
• 径向基核 (RBF) \(K(x,xi)=\exp(- \parallel x - xi \parallel / 2 \sigma^2)\)

实验报告 ¶

机器学习 -- 支持向量机

892 KB / 9 P / 2023-10-20

下载

神经网络 ¶

神经元模型 MP ¶

• 包含输入输出与计算功能的模型

单层神经网络（感知器）¶

• 与神经元模型不同，感知器中的权值是通过训练得到的
• 感知器可以做（简单）线性分类任务
• 用决策边界来表达分类效果
• XOR 无法解决

两层神经网络（多层感知器）¶

结构 ¶

• 两层神经网络除了输入层和输出层，还增加一个中间层
• 中间层和输出层都是计算层
• 通过扩展上个单元的单层神经网络，在右边新加一个层次

隐藏层的节点数设计 ¶

• 输入层的节点数需要与特征的维度匹配
• 输出层的节点数需要与目标的维度匹配
• 中间层的节点数由设计者决定
• 较好的方法就是预先设定几个可选值，通过切换不同值来看整个模型的预测效果，简称 Grid Search

两层神经网络训练 ¶

训练与损失函数 ¶

• 首先给所有参数赋上随机值，使用这些参数值来预测训练数据中的样本，样本的预测目标为 \(y_p\)，真实目标为 \(y\)。那么定义一个值 \(loss = (y_p-y)/2\)
• loss 称之为损失，目标就是使对所有训练数据的损失和尽可能的小
• 如果将先前的神经网络预测的矩阵公式带入到 \(y_p\) 中（因为有 \(z=y_p\)），那么我们可以把损失写为关于参数的函数，这个函数称之为损失函数 (loss function)

神经网络优化问题 ¶

• 一般使用梯度下降法来优化，因为代价很大，所以需要使用反向传播算法
• 反向传播算法利用神经网络的结构进行的计算，不一次计算所有的梯度，而是从后往前
• 反向传播的依据：链式法则

框架 ¶

• Pytorch

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
...
loss.backward()

• TensorFlow

train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)

实验报告 ¶

机器学习 -- 神经网络

855 KB / 7 P / 2023-10-20

下载

识别系统的模型选择与评估 ¶

• 误差很大时
  • 获取更多的训练数据
  • 尝试减少特征
  • 大量时间（>6 个月）可能都在做这些调整
  • 尝试增加多项式特征
  • 尝试降低 / 提高 \(\lambda\)

训练集、测试集、校验集 ¶

• 高阶模型能够很好地拟合，但对不在训练集中的新样本缺乏泛化能力
• 可以考虑打乱数据，以增强泛化能力

错误率 & 误差 ¶

• 错误率：错分样本的占比
• 误差：样本真实输出与预测输出之间的差异
  • 训练（经验）误差：训练集
  • 测试误差：测试集
  • 泛化误差：除训练集外所有样本

经验误差与过拟合 ¶

• 过拟合
  • 学习器把所有训练样本学习的“太好”，将训练样本本身的特点当作所有样本的一般性质，导致泛化性能下降
    • 优化目标加正则项
    • early stop
• 欠拟合
  • 对训练样本的一般性质尚未学好
    • 决策树：拓展分支
    • 神经网络：增加训练轮数

常用评估方法 ¶

留出法 ¶

• 直接将数据集划分为两个互斥集合
• 训练 / 测试集划分要尽可能保持数据分布的一致性
• 一般若干次随机划分，重复实验取平均值
• 训练 / 测试样本比例通常为 2:1-4:1

交叉验证法 ¶

• 将数据集划分为 k 个大小相似的互斥子集
• 每次用 k-1 个子集的并集作为训练集，余下的子集作为测试集
• 进行 k 次训练和测试，最终返回 k 次测试结果的均值
• 一般 k 为 10

自助法 ¶

• 实际模型与预期模型都使用 m 个训练样本
• 约有 1/3 的样本没在训练集中出现
• 从初始数据集中产生多个不同的训练集，对集成学习有很大的好处
• 自助法在数据集较小，难以有效划分训练 / 测试集时很有用
• 自助法产生的数据集改变了初始数据集的分布，会引入估计偏差，在数据量足够时，留出法和交叉验证法更常用

性能度量 ¶

• 分类任务最常用的是错误率和精度
  • 错误率：\(E(f;D)=\frac{1}{m} \sum_{i=1}^m (f(\mathbf{x}_i) \ne y_i)\)
  • 精度：\(acc(f;D)=\frac{1}{m} \sum_{i=1}^m (f(\mathbf{x}_i) = y_i)=1-E(f;D)\)
• 回归任务最常用的是均方误差 \(E(f;D)=\frac{1}{m} \sum_{i=1}^m (f(\mathbf{x}_i) - y_i)^2\)
• 混淆矩阵 Confusion matrix
  • 查准率 Precision：\(P=\frac{TP}{TP+FP}\)
  • 查全率 Recall：\(P=\frac{TP}{TP+FN}\)
• P-R 曲线：根据学习器的预测结果按正例可能性大小对样例进行排序，并逐个把样本作为正例进行预测，则可以得到查准率 - 查全率
• F1 Score：\(F1 Score=2\frac{PR}{P+R}\)
  • 更一般的形式 \(F_\beta = \frac{(1+\beta^2) \times P \times R}{(\beta^2 \times P) + R}\)
  • \(\beta=1\)：标准 F1
  • \(\beta<1\)：更重视查准率（商品推荐系统）
  • \(\beta>1\)：更重视查全率（逃犯信息检索）
• ROC 曲线：受试者工作特征曲线
  • 横轴：\(FPR=\frac{FP}{FP+TN}\)
  • 纵轴：\(TPR=\frac{TP}{TP+FN}\)
  • AUC：ROC 曲线下的面积，越大越好
• 代价敏感错误率

比较校验 ¶

• 假设校验
• 二项校验
• t 检验
• 交叉验证 t 检验
• McNemar 检验
• Friedman 检验
• Nemenyi 检验

聚类 ¶