模式识别 ¶

模式识别的概述 ¶

模式和模式识别的概念 ¶

• 模式：对某些感兴趣的客体的定量的或结构的描述。模式类是具有某些共同特性的模式的集合。
• 模式识别：研究一种自动技术，依靠这种技术，计算机将自动地（或人尽量少地干涉）把待别识模式分配到各自的模式类中去。

模式识别系统组成 ¶

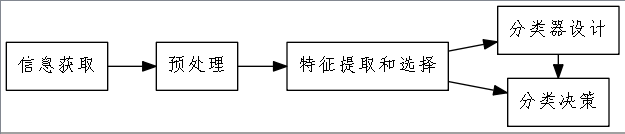
注意“处理”与“识别”两个概念的区别

模式识别的分类 ¶

1. 从理论上分类
   1. 统计模式识别
   2. 句法模式识别（结构模式识别）
   3. 模糊模式识别
   4. 神经网络模式识别
2. 从实现方法分类
   1. 监督分类
   2. 非监督分类

模式识别的应用 ¶

聚类分析 ¶

距离聚类的概念 ¶

1. 概念：物以类聚
   • 聚类分析：根据模式之间的相似性对模式进行分类，是一种非监督分类方法。
2. 相似度含义
   • 有 n 个特征则组成 n 维向量 \(X=[x_1, x_2, ..., x_n]^{\top}\) 称为该样本的特征向量。它相当于特征空间中的一个点，以特征空间中，点间的距离函数作为模式相似度的测量，以“距离”作为模式分类的依据，距离越小，越相似

聚类分析是否有效，与模式特征向量的分布形式有很大关系。选取的特征向量是否合适非常关键。

相似性测度和聚类准则 ¶

相似性测度 ¶

衡量模式之间相似性的一种尺度。如：距离。

• 欧氏距离

  设 \(X_1, X_2\) 为两个 n 维模式样本，\(X_1 = [x_{11}, x_{12}, ..., x_{1n}]^{\top}, X_2 = [x_{21}, x_{22}, ..., x_{2n}]^{\top}\)，欧氏距离定义为 :

  \[ D(X_1, X_2) = \parallel X_1 - X_2 \parallel = \sqrt{(X_1 - X_2)^{\top}(X_1-X_2)} \]

  距离越小越相似。

• 马式距离

  平方表达式：\(D^2=(X_1-X_2)^{\top}C^{-1}(X_1-X_2)\)

  令 \(M:\) 均值向量 M_Mean，\(C:\) 该类模式总体的协方差矩阵 C_covariance。

  对 n 维向量 :\(X=[x_1, ..., x_n]^{\top},M=[m_1,...,m_n]^{\top}\)

  \[ C = E\{(X-M)(X-M)^{\top}\} \\ = E \{ \begin{bmatrix} (x_1-m_1) \\ (x_2-m_2) \\ ... \\ (x_n-m_n) \end{bmatrix} [(x_1-m_1)(x_2-m_2)\cdot \cdot \cdot (x_n-m_n)]\} \\ = \begin{bmatrix} \sigma_{11}^2 & \sigma_{12}^2 & ... & \sigma_{1n}^2 \\ \sigma_{21}^2 & \sigma_{22}^2 & ... & \sigma_{2n}^2 \\ ... & ... & ... & ... \\ \sigma_{n1}^2 & \sigma_{n2}^2 & ... & \sigma_{nn}^2 \end{bmatrix} \]

  表示的概念是各分量上模式样本到均值的距离，也就是在各维上模式的分散情况。\(\sigma_{jk}^2\) 越大，离均值越远。

  当 \(C=I\) 时，马式距离就是欧氏距离。

  特点：

  1. 马式距离的计算是建立在总体样本的基础上。同样的两个样本，放入两个不同的总体中，最后计算得出两个样本间的马式距离通常是不相同的；
  2. 不受量纲的影响，两点之间的马式距离与原始数据的测量单位无关；
  3. 马式距离可以排出变量之间的相关性的干扰；
  4. 夸大了变化微小的变量的作用。

• 明氏距离

  n 维模式样本向量 \(X_i、X_j\) 间的明氏距离表示为：

  \[ D_m(X_i, X_j)=[\sum_{k=1}^n|x_{ik}-x_{jk}|^m]^{\frac{1}{m}} \]

  式中，\(x_{ik}, x_{jk}\) 分别表示 \(X_i\) 和 \(X_j\) 的第 k 个分量。

  当 \(m=2\) 时，明氏距离为欧氏距离。 当\(m=1\)时，\(D_1(X_i, X_j)=\sum_{k=1}^n|x_{ik}-x_{jk}|\)，为街坊距离。

• 汉明距离

  设 \(X_i、X_j\) 为 n 维二值 (1 或 -1) 模式样本向量，则 汉明距离为\(D_h(X_i, X_j)=\frac{1}{2}(n-\sum_{k=1}^n x_{ik}*x_{jk})\)

  式中，\(x_{ik}, x_{jk}\) 分别表示 \(X_i\) 和 \(X_j\) 的第 k 个分量。

  两个模式向量的各分量取值均不同：\(D_h(X_i, X_j)=n\)，全相同：\(D_h(X_i, X_j)=0\)

• 角度相似性函数

  \[ S(X_i, X_j) = \frac{X_i^{\top}X_j}{\parallel X_i \parallel \cdot \parallel X_j \parallel} \]

  是模式向量 \(X_i, X_j\) 之间的夹角的余弦。

• Tanimoto 测度

  用于 0,1 二值特征的情况 ,

  \[ S(X_i,X_j)=\frac{X_i^{\top}X_j}{X_i^{\top}X_i+X_j^{\top}X_j-X_i^{\top}X_j} \\ \ \\ = \frac{X_i,X_j中共有的特征数目}{X_i和X_j中占有的特征数目的总数} \]

  相似性测度函数的共同点都涉及到把两个相比较的向量 \(X_i,X_j\) 的分量值组合起来，但怎样组合并无普遍有效的方法，对具体的模式分类，需视情况作适当选择。

聚类准则 ¶

根据相似性测度确定的，衡量模式之间是否相似的标准。即把不同模式聚为一类还是归为不同类的准则。

确定聚类准则的两种方式：

1. 阈值准则：根据规定的距离阈值进行分类的准则
2. 函数准则：利用聚类准则函数进行分类的准则
   • 聚类准则函数：在聚类分析中，表示模式类间相似或差异性的函数
   • 它应是模式样本集 \(\{X\}\) 和模式类别 \(\{S_j,j=1,2,..,c\}\) 的函数。可使聚类分析转化为寻找准则函数极值的最优化问题。一种常用的指标是误差平方之和。

基于距离阈值的聚类算法 ¶

近邻聚类法 ¶

1. 问题：有 \(N\) 个待分类的模式 \(\{X_1, X_2, ..., X_N\}\)，要求按距离阈值 \(T\) 分类到以 \(Z_1, Z_2,...\) 为聚类中心的模式类中。
2. 算法描述
   1. 任取样本 \(X_i\) 作为第一个聚类中心的初始值，如令 \(Z_1=X_1\)
   2. 计算样本 \(X_2\) 到 \(Z_1\) 的欧氏距离 \(D_{21}=\parallel X_2 - Z_1 \parallel\)，若 \(D_{21}>T\)，定义一新的聚类中心 \(Z_2=X_2\)；否则 \(X_2 \in\) 以 \(Z_1\) 为中心的聚类。
   3. 假设已有聚类中心 \(Z_1、Z_2\)，计算 \(D_{31}=\parallel X_3 - Z_1 \parallel\) 和 \(D_{32}=\parallel X_3 - Z_2 \parallel\)，若 \(D_{31}>T\) 且 \(D_{32} > T\)，则建立第三个聚类中心 \(Z_3=X_3\)；否则 \(X_3 \in\) 离 \(Z_1\) 和 \(Z_2\) 中最近者（最近邻的聚类中心）。
   4. 依此类推，直到将所有的 \(N\) 个样本都进行分类
3. 算法特点
   1. 局限性：很大程度上依赖于第一个聚类中心的位置选择、待分类模式样本的排列次序、距离阈值 \(T\) 的大小以及样本分布的几何性质等。
   2. 优点：计算简单。（一种虽粗糙但快速的方法）

最大最小算法（小中取大距离算法）¶

1. 问题：已知 \(N\) 个待分类的模式 \(\{X_1, X_2, ..., X_N\}\)，分类到聚类中心 \(Z_1, Z_2, ...\) 对应的类别中
2. 算法描述
   1. 选任意一模式样本作为第一聚类中心 \(Z_1\)
   2. 选择离 \(Z_1\) 距离最远的样本作为第二聚类中心 \(Z_2\)
   3. 逐个计算各模式样本与已确定的所有聚类中心之间的距离，并选出其中的最小距离。例如聚类中心数 \(k=2\) 时，计算 \(D_{i1}=\parallel X_i - Z_1 \parallel\), \(D_{i2}=\parallel X_i - Z_2 \parallel\)，\(\min\{D_{i1}, D_{i2}\}, i=1,...,N\)(N 个最小距离 )
   4. 在所有最小距离中选出最大距离，如该最大值达到 \(\parallel Z_1 - Z_2 \parallel\) 的一定分数比值（阈值 \(T\)）以上，则相应的样本点取为新的聚类中心，返回 3；否则结束
   5. 重复步骤 3、4，直到没有新的聚类中心出现为止
   6. 将样本 \(\{X_1, i=1,2,..,N\}\) 按最近距离划分到相应聚类中心对应的类别中
3. 总结：先找中心后分类；关键：怎么开新类，聚类中心如何定

层次聚类法 ¶

每个样本先自成一类，然后按距离准则逐步合并，减少类数

1. 算法描述
   1. \(N\) 个初始模式样本自成一类，即建 \(N\) 类：\(G_1(0), G_2(0), ..., G_N(0)\)，计算各类之间（即各样本间）的距离，得一 \(N \times N\) 维距离矩阵 \(\mathbf{D}(0)\)。\(“0”\) 表示初始状态
   2. 假设已求得距离矩阵 \(\mathbf{D}(n)\)（n 为逐次聚类合并的次数），找出 \(\mathbf{D}(n)\) 中的最小元素，将其对应的两类合并成一类。由此建立新的分类：\(G_1(n+1), G_2(n+1),...\)
   3. 计算合并后新类别之间的距离，得 \(\mathbf{D}(n+1)\)
   4. 跳到第 2 步，重复计算及合并
   5. 结束条件
      1. 取距离阈值 \(T\)，当 \(\mathbf{D}(n)\) 的最小分量超过给定值 \(T\) 时，算法停止，所得即为聚类结果
      2. 或不设阈值 \(T\)，一直将全部样本聚成一类为止，输出聚类的分级树

2. 问题讨论：类间距离计算准则

   1. 最短距离法 如\(H、K\)是两个聚类，则两类间的最短距离定义为:

      \[ D_{HK} = \min\{D(\mathbf{X}_H-\mathbf{X}_K)\} \ \ \ \mathbf{X}_H \in H, \mathbf{X}_K \in K \]

   2. 最长距离法

      \[ D_{HK} = \max\{D(\mathbf{X}_H-\mathbf{X}_K)\} \ \ \ \mathbf{X}_H \in H, \mathbf{X}_K \in K \\ 若 K 类由 I、J 两类合并而成则 \\ D_{HK} = \max\{D_{HI}, D_{HJ}\} \]

   3. 中间距离法 介于最长与最短的距离之间

      \[ D_{HK}=\sqrt{\frac{1}{2} D_{HI}^2+\frac{1}{2}D_{HJ}^2-\frac{1}{4}D_{IJ}^2} \]

   4. 重心法 将每类中包含的样本数考虑进去。若\(I\)类中有\(n_I\)个样本，若\(J\)类中有\(n_J\)个样本

      \[ D_{HK}=\sqrt{\frac{n_I}{n_I+n_J} D_{HI}^2+\frac{n_J}{n_I+n_J}D_{HJ}^2-\frac{n_In_J}{n_I+n_J}D_{IJ}^2} \]

   5. 类平均距离法

      \[ D_{HK}=\sqrt{\frac{1}{n_Hn_K} \sum_{i \in H,j \in K}d_{ij}^2} \]

      \(d_{ij}\)：\(H\) 类任一样本 \(X_i\) 和 \(K\) 类任一样本 \(X_i\) 之间的欧氏距离平方

      若 \(K\) 类由 \(I\) 类和 \(J\) 类合并产生，则递推式为

      \[ D_{HK}=\sqrt{\frac{n_I}{n_I+n_J} D_{HI}^2+\frac{n_J}{n_I+n_J}D_{HJ}^2} \]

动态聚类法 ¶

两种常用的算法：

• \(K\)- 均值算法 ( 或 \(C\)- 均值算法 )
• 迭代自组织的数据分析算法

K- 均值算法 ¶

• 基于使聚类准则函数最小化
• 准则函数：聚类集中每一样本点到该类中心到距离平方和
• 对于第 j 聚类集，准则函数定义为 \(J_j = \sum_{i=1}^{N_j} \parallel X_i - Z_j \parallel ^2，\ \ \ X_i \in S_j\)
  • \(S_j\): 第 j 个聚类集，聚类中心为 \(Z_j\)
  • \(N_j\): 第 j 个聚类集 \(S_j\) 中所包含的样本个数

• 对所有 \(K\) 个模式类有 \(J = \sum_{j=1}^{K} \sum_{i=1}^{N_j} \parallel X_i - Z_j \parallel ^2, \ \ \ X_i \in S_j\)

• 聚类准则：聚类中心的选择应使准则函数 \(J\) 极小，即使 \(J_j\) 的值很小

• 让 \(\frac{\partial J_j}{\partial \mathbf{Z}_j}=0\)，解得 \(\mathbf{Z}_j = \frac{1}{N_j} \sum_{i=1}^{N_j} \mathbf{X_i}, \ \ \ \mathbf{X}_i \in S_j\)

• 算法描述 :

  1. 任选 K 个初始聚类中心：\(\mathbf{Z}_1(1), \mathbf{Z}_2(1), ..., \mathbf{Z}_K(1)\) 括号内序号：迭代运算的次序号
  2. 按最小距离原则将其余样品分配到 K 个聚类中心中的某一个，即 \(\min\{\parallel X - Z_i(k) \parallel, i=1,2,...,K\}=\parallel X-Z_j(k) \parallel=D_j(k)，则 X \in S_j(k)\)，注意，k 是迭代运算次序号，K 是聚类中心个数
  3. 计算各个聚类中心的新向量值 : \(Z_j(k+1) \ \ j=1,2,...,K\)
  \[ Z_j(k+1) = \frac{1}{N_j} \sum_{X \in S_j(k)} \mathbf{X} \ \ \ j=1,2,...,K \]

  \(N_j\): 第 j 类的样本数

  4. 判断
     • 如果 \(Z_j(k+1) \ne Z_j(k) \ \ j=1,2,...,K\)，则回到 2，将模式样本逐个重新分类，重复迭代计算
     • 如果 \(Z_j(k+1) = Z_j(k) \ \ j=1,2,...,K\)，算法收敛，计算完毕

迭代自组织的数据分析算法 ¶

• 算法特点
  • 加入了试探性步骤，组成人机交互的结构
  • 可以通过类的自动合并与分裂得到较合理的类别数
• 与 K- 均值算法
  • 相似：聚类中心的位置均通过样本均值的迭代运算决定
  • 相异：K- 均值算法的聚类中心个数不变，但 ISODATA 算法不变

• 算法描述

  1. 预选 \(N_C\) 个聚类中心 \(\{Z_1, Z_2, ..., Z_{N_C}\}\)，\(N_C\) 也是聚类过程中实际的聚类中心个数
  2. 把 N 个样本按最近邻规则分配到 \(N_C\) 个聚类中
  \[ 若 \ \ \ \parallel X - Z_j \parallel = \min\{\parallel X - Z_i, i = 1, ,2, .., N_C\} \\ 则 \ \ \ X \in S_j \]
  3. 若 \(S_j\) 中的样本数 \(N_j < \theta_N\)，则取消该类，并且 \(N_C\) 减去 1
  4. 修正各聚类中心值 \(Z_j = \frac{1}{N_j} \sum_{X \in S_j} X \ \ \ j=1,2,...,N_C\)
  5. 计算 \(S_j\) 的类内的平均距离 \(\bar{D_j} = \frac{1}{N_j} \sum_{X \in S_j} \parallel X - Z_j \parallel \ \ \ j=1,2,...,N_C\)
  6. 计算总体平均距离
  7. 判断当前是分裂还是合并，决定迭代步骤等
     1. 若 \(N_C \le K/2\)，进入分裂
     2. 如果迭代次数是偶数或 \(N_C \ge 2K\)，则合并否则分裂
  8. 计算每个聚类中样本距离的标准差向量
  9. 求每个标准差向量的最大分量
  10. 太长了。。。
  11. 全是公式。。。

判别函数 ¶

判别函数 ¶

1. 定义：直接用来对模式进行分类的准则函数。若分属于 \(\omega_1, \omega_2\) 的两类模式可用一方程 \(d(X)=0\) 来划分，那么称 \(d(X)\) 为判别函数。
2. 确定判别函数的两个因素
   1. 判决函数 \(d(X)\) 的几何性质。它可以是线性的或非线性的函数，维数在特征提取时已经确定
   2. 判决函数 \(d(X)\) 的系数，用所给的模式样本确定

线性判别函数 ¶

一般形式 ¶

将二维形式推广到 n 维，线性判别函数的一般形式为

增广向量的形式 \(d(X)=W^{\top}X\)

性质 ¶

1. 两类情况

2. 多类情况

• \(\omega_i \sqrt{\omega_i}\) 两分法
  • 用线性判别函数将属于 \(\omega_i\) 类的模式与其余不属于 \(\omega_i\) 类的模式分开
• \(\omega_i \omega_i\) 两分法
  • 一个判别界面只能分开两个类别，不能把其余所有的类别都分开。判决函数为 \(d_{ij}(X)=W_{ij}^{\top}X\)
  • 性质：\(d_{ij}(X) > 0, \forall j \ne i; i, j = 1,2,...,M，若X \in \omega_i\)

广义线性判别函数 ¶

• 目的：对非线性边界，通过某映射，把模式空间 \(X\) 变成 \(X^*\)，以便将 \(X\) 空间中非线性可分的模式集，变成在 \(X^*\) 空间中线性可分的模式集

非线性多项式函数 ¶

• 非线性判别函数的形式之一是非线性多项式函数
• 设一训练用模式集，\(\{X\}\) 在模式空间 \(X\) 中线性不可分，非线性判别函数形式如下：

• 广义形式的模式向量定义为：

线性判别函数的几何性质 ¶

• 模式空间与超平面
• 权空间和权向量解

感知器算法 ¶