矩阵代数基础

Abstract

矩阵是描述和求解线性方程组最基本和最有用的数学工具

• 数学运算: 转置、内积、外积、逆矩阵、广义逆矩阵等
• 标量函数：范数、二次型、行列式、特征值、秩和迹
• 特殊运算: 直和、直积、Hadamard 积、Kronecker 积、向量化

矩阵的基本运算

矩阵与向量

\(m \times n\)的线性方程组，使用\(m\)个方程描述\(n\)个未知量之间的线性关系。用矩阵-向量形式表示为\(Ax = b\)，称为\(m \times n\)矩阵。特殊的有行向量和列向量（包括实数和复数）。

• \(n \times n\)矩阵的主对角线是指从左上角到右下角相连接的线段，次对角线（交叉对角线）是从右上角到左下角。
• 主对角线以外元素全部为0的\(n \times n\)的矩阵称为对角矩阵。
• 对角矩阵主对角线元素全部位 1，称为单位矩阵\(I_{n \times n}\)。
• 所有元素为 0 的\(m \times n\)矩阵称为零矩阵\(O_{m \times n}\)。
• 一个全部元素为零的向量称为零向量。

矩阵的基本运算

• \(A=[a_{ij}]\)的转置记作\(A^{\top}\)，元素定义为\([A^{\top}]_{i,j}=a_{ji}\)
• \(A=[a_{ij}]\)的复数共轭记作\(A^*\)，元素定义为\([A^*]_{ij}=a_{ij}^*\)
• \(A=[a_{ij}]\)的(复)共轭转置记作\(A^H\)，元素定义为\([A^H]_{ij}=a_{ji}^*\)，（共轭转置又叫 Hlermitian 伴随/转置/共轭）
• 满足\(A^{\top}=A\)的正方实矩阵和\(A^H=A\)的正方复矩阵分别称为对称矩阵和 Hermitian 矩阵(复共轭对称矩阵)，共轭转置和转置的关系:\(A^H=(A^*)^{\top}=(A^{\top})^*\)
• 矩阵满足与标量/矩阵/向量之间的加法、乘法（矩阵乘法不满足交换律）
• 矩阵与向量的乘法\(Ax=y\)可视为向量\(x\)的线性变换，\(A\)称为线性变换矩阵
• 如果\(A\)可逆，则存在\(A^{-1}\)使得\(A^{-1}A=I\)，称\(A^{-1}\)是\(A\)的逆矩阵
• 矩阵的共轭、转罝和共轭转置满足分配律：\((A+B)^x=A^x+B^x，x \in (*,T,H)\)
• 矩阵乘积的转置、共轭转置和逆矩阵满足关系式：\((AB)^x=B^xA^x，x \in (T,H,-1)\)
• 共轭、转置和共轭转置等符号均可与求逆符号交换：\((A^x)^{-1}=(A^{-1})^x，x \in (*,T,H)\)
• 若\(A\)可逆，对于 Hermitian 矩阵\(B=A^HA\)，有\(A^{-H}BA^{-1}=A^{-H}A^HAA^{-1}=I\)
• 若$A_{n \time n}为幂等矩阵，则
  • \(A^n = A\)
  • \(I-A\)为幂等矩阵（\(A-I\)不一定是幂等矩阵）
  • \(A^H\)为幂等矩阵
  • \(I-A^H\)为幂等矩阵
  • 若\(B\)也为幂等矩阵，并且\(AB=BA\)，则\(AB\)为幂等矩阵
  • \(A(I-A)=O\)（零矩阵）
  • \((I-A)A=O\)（零矩阵）
  • 函数\(f(sI+tA)=(I-A)f(s)+Af(s+t)\)
• 若\(A_{n \times n}\)为对合矩阵或幂单矩阵，则
  • \(f(sI=tA)=\frac{1}{2}[(I+A)f(s+t)+(I-A)f(s-t)]\)
  • 矩阵\(A\)是对合矩阵，当且仅当\(\frac{1}{2}(A+I)\)为幂等矩阵
• 若\(A_{n \times n}\)为幂零矩阵，则
  • \(f(sI+tA)=If(s)+tAf^\prime(s)\)
• 除了矩阵的基本运算，还有矩阵/三角/指数/对数函数、导数、积分等等

向量的线性无关性与非奇异矩阵

• 一组\(m\)维向量\(\{u_1, ..., u_n\}\)称为线性无关，则方程\(c_1u_1+...+c_nu_n=0\)只有零解\(c_1=...=c_n=0\)，反之线性相关。矩阵\(A\)是非奇异的，当且仅当\(Ax=0\)只有零解，反之矩阵是奇异的
• \(A_{n \times n}=[a_1,...,a_n]\)是非奇异的，当且仅当它的\(n\)个列向量\(a_1,...,a_n\)线性无关。

向量空间、线性映射与 Hilbert 空间

向量空间

• 以向量为元素的集合\(V\)称为向量空间。如果\(V\)是一个向量空间，则：
  • 零向量\(0\)是唯一的
  • 对每一个向量\(y\)，加法的逆运算\(-y\)是唯一的
  • 对每一个向量\(y\)，恒有\(0y=0\)
  • 对每一个标量 a，恒有\(a0=0\)
  • 若\(ay=0\)，则\(a=0\)或者\(y=0\)
  • \((-1)y=-y\)
• 令\(V\)和\(W\)是两个向量空间，若\(W\)是\(V\)中一个非空的子集合，则称子集合\(W\)是\(V\)的一个子空间
• \(R^n\)的子集合\(W\)是\(R^n\)的一个字空间，当且仅当满足以下条件：
  • 当向量\(x,y\)属于\(W\)，则\(x+y\)也属于\(W\)，即满足加法的闭合性
  • 当\(x \in W\)，且 a 为标量，则\(ax\)也属于\(W\)，即满足与标量乘积的闭合性
  • 零向量\(0\)是\(W\)的元素
• 若\(A\)和\(B\)是向量空间\(V\)的两个子空问，并满足\(V=A+B\)和\(A \cap B=\{0\}\) ，则称\(V\)是子空间\(A\)和\(B\)的直接求和，简称直和(direetsum)，记作\(V=A \oplus B\)。

线性映射

\(T:\ V \to W\)称为子空间\(V\)到子空间\(W\)的映射。它表示将子空间\(V\)的每一个向量变成子空间\(W\)的一个相对应向量的一种规则。于是，若\(v \in V\)和\(w \in W\)，则向量\(w\)是\(v\)的映射或变换，即有\(w = T(v)\)，并称子空间\(V\)是映射\(T\)的始集或丁一宇，称\(W\)是映射的终集或上域。

令\(V\)和以是两个向量空间，\(T:V \to W\)为一线性变换:

1. 若\(M\)是\(V\)的线性子空间，则\(T(M)\)是\(W\)的线性子空间；
2. 若\(N\)是\(W\)的线性子空间，則线性反变换\(T^{-1}(N)\)是\(V\)的线性子空间。

内积空间、赋范空问与Hilbert 空间

• （内积与内积向量空间）若对所有\(x,y,z \in V\)和\(\alpha,\beta \in K\)，映射函数\(<\cdot,\cdot>:V \times V \to K\)满足一下三条公理：
  • 共轭对称性 \(<x,y>=<y,x>^*\)
  • 第一变元的线性性 \(<\alpha x+\beta y,z>=\alpha <x,z> + \beta <y,z>\)
  • 非负性 \(<x,x> \ge 0\)，并且\(<x,x> = 0 \leftrightarrow x=0\)（严格正性）

两个向量的内积可以度量它们之问的夹角：\(\cos \theta = \frac{<x,y>}{\sqrt{<x,x>}\sqrt{<y,y>}}\)

• （范数和赋范向量空间）令\(V\)是一(实或复)向量空间。向量\(x\)的范数是一实函数\(p(x):V \to R\)，若对所有向量\(x,y \in V\)和任意一个标量\(c \in K\)(其中\(K\)表示\(R\)或\(C\))，则：

  • 非负性：\(p(x) \ge 0\)，并且\(p(x)=0 \Leftrightarrow x = 0\)
  • 齐次性：\(p(cx)=|c|\cdot p(x)\)对所有复常数\(c\)成立
  • 三角不等式：\(p(x+y) \le p(x)+p(y)\)

  • 最常用的向量范数为 Euclidean 范数或者\(L_2\)范数，记作\(\parallel \cdot \parallel_2\)，定义为

    \[ \parallel x \parallel _E = \parallel x \parallel _2 = \sqrt{x_1^2+...+x_m^2} \]

  • \(L_2\)范数可以直接度量一个向量\(x\)的长度\(size(x)=\parallel x \parallel_2\)，两个向量之间的距离\(d(x,y)=\parallel x-y \parallel_2\)

  • （向量\(x \in V\)的半范数/伪范数）若对所有向量\(x,y \in V\)和一个标量\(c\)，满足
  • \(p(x) \ge 0\)
  • \(p(cx)=|c| \cdot p(x)\)
  • \(p(x+y) \le p(x)+p(y)\)
  • （向量\(x \in V\)的拟范数）若对所有向量\(x,y \in V\)和一个标量\(c\)，满足
  • \(p(x) \ge 0\)，且\(p(x) = 0 \Leftrightarrow x = 0\)
  • \(p(cx)=|c| \cdot p(x)\)
  • \(p(x+y) \le C(p(x)+p(y))\)，其中\(C \ne 1\)为某个正实数
  • （完备性）一个向量空间\(V\)称为完备向量空间，若对于\(V\)中的每一个 Cauchy 序列\(\{ v_n \}_{n=1}^{\infty} \subset V\)，在向量空间\(V\)内存在一个元素\(v\)，使得\(\lim_{n \to \infty} v_n \to v\)，即\(V\)内的每一个 Cauchy 序列都收敛在向量空间\(V\)内。

• （伴随算子）令\(T\)是 Hilbert 空间\(H\)内的有界线性算子。若\(<Tx,y>=<x,T^*y>\)对所有向量\(x,y \in H\)成立，则称\(T^*\)是\(T\)的伴随算子(adjoint operator)。

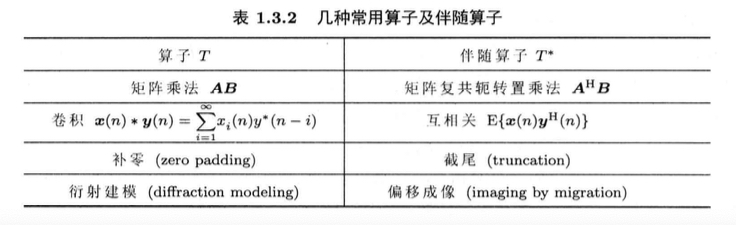
内积与范数

向量的内积与范数

\(n\)阶复向量\(x=[x_1,...,x_n]^{\top},y=[y_1,...,y_n]^{\top}\)之间的内积\(<x,y>=x^Hy=\sum_{i=1}^n x_i^*y_i\)称为典范内积。加权内积\(<x,y>=x^HGy\)，其中\(G\)为正定的 Hermitian 矩阵。

在实和复内积空间里，范数具有以下性质：

1. \(\parallel 0 \parallel = 0\)，并且\(\parallel x \parallel > 0，\forall x \ne 0\)
2. \(\parallel cx \parallel = |c| \cdot \parallel x \parallel\)对所有向量\(x\)和标量 c 成立

3. 范数服从极化恒等式：

   \[ <x,y> =\frac{1}{4}(\parallel x + y \parallel^2-\parallel x - y \parallel^2), \forall x,y（实内积空间）\\ <x,y> =\frac{1}{4}(\parallel x + y \parallel^2-\parallel x - y \parallel^2 - j \parallel x+jy \parallel^2+j \parallel x-jy \parallel^2), \forall x,y（复内积空间） \]

4. 范数服从平行四边形法则:

   \[ \parallel x+y \parallel^2 + \parallel x - y \parallel^2 = 2(\parallel x \parallel^2+\parallel y \parallel^2), \forall x,y \]

5. 范数满足三角不等式\(\parallel x+y \parallel \le \parallel x \parallel + \parallel y \parallel, \forall x,y\)

6. 范数服从 Cauchy-Schwartz 不等式\(|<x,y>| \le \parallel x \parallel \cdot \parallel y \parallel\)

常数向量的典范内积与范数

1. \(L_0\)范数 \(\parallel x \parallel_0 \overset{def}{=}\)非零元素的个数
2. \(L_1\)范数 \(\parallel x \parallel_1 \overset{def}{=} \sum_{i=1}^m |x_i|\)
3. \(L_2\)范数 \(\parallel x \parallel_2 = (|x_1|^2+...+|x_m|^2)^{\frac{1}{2}}\)
4. \(L_\infty\)范数 \(\parallel x \parallel_\infty = \max\{|x_1|, ..., |x_m|\}\)
5. \(L_p\)范数 \(\parallel x \parallel_p = (\sum_{i=1}^m |x_i|^p)^{\frac{1}{p}}\)

函数向量的内积与范数

若\(x(t)\)和\(y(t)\)分别是变量\(t\)的函数变量，则内积定义为

\[ <x(t),y(t)> \overset{def}{=} \int_{a}^{b} x^H(t)y(t)dt \]

随机向量的内积与范数

若\(x(\xi)\)和\(y(\xi)\)分别是样本变量\(\xi\)随机变量，则内积定义为

\[ <x(\xi),y(\xi)> \overset{def}{=} E\{x^H(\xi)y(\xi)\} \]

矩阵的内积与范数

将向量的内积与范数加以推广。

矩阵的范数有三种主要类型:诱导范数、元素形式范数和 Schatten 范数。

随机向量

概率论知识。

矩阵的性能指标

• 二次型
• 特征值
• 迹
• 秩

逆矩阵与伪逆矩阵

主要讨论非奇异的正方矩阵\(A\)的逆矩阵\(A^{-1}\)

Moore-Penrose 逆矩阵

主要讨论一个秩稀缺的矩阵是否存在逆矩阵，如果存在需要满足什么条件。

矩阵的直和与Hadamard 积

矩阵的直和

\(m \times m\)矩阵的\(A\)与\(n \times n\)矩阵的\(B\)的直和记作\(A \oplus B\)，即

\[ A \oplus B = \begin{bmatrix} A & O_{m \times n} \\ O_{n \times m} & B \end{bmatrix} \]

Hadamard 积

\(m \times n\)矩阵的\(A=[a_{ij}]\)与\(m \times n\)矩阵的\(B=[b_{ij}]\)的 Hadamard 积记作\(A * B\)，元素定义为\((A*B)_{ij}=a_{ij}b_{ij}\)。即 Hadamard 积食一种映射\(R^{m \times n} \times R^{m \times n} \to R^{m \times n}\)

Kronecker 积与Khatri-Rao 积

Kronecker 积

Kronecker 积分为右和左两种 Kronecker 积。

例如右 Kronecker 积记作\(A \oplus B\)，定义为：

\[ A \oplus B = [a_1B, ..., a_nB]=[a_{ij}B]_{i=1,j=1}^{m,n}= \begin{bmatrix} a_{11}B &a_{12}B &... &a_{1n}B \\ a_{21}B &a_{22}B &... &a_{2n}B \\ ... & ... & ... &... \\ a_{m1}B &a_{m2}B & ... &a_{mn}B \end{bmatrix} \]

Kronecker 积也称直积(direct product)或者张量积(tensor product)1

Khatri-Rao 积

两个具有相同列数的矩阵\(G \in R^{p \times n}\)和\(F \in R^{q\times n}\)的 Khatri-Rao 积记作\(F \odot G\)，定义为

\[ F \odot G = [f_1 \oplus g_1, f_2 \oplus g_2, ..., f_n \oplus g_n] \in R^{pq \times n} \]

它由两个矩阵的对应列向量的Kronecker 积排列而成。因此，Khatri-Rao 积又叫对应列 Kronecker 积。

向量化与矩阵化

矩阵的向量化\(vec(A)\)是一线性变换，将\(A\)按列堆栈（当然也可以按行堆栈）排列成一个\(mn \times 1\)向量。即

\[vec(A)=[a_{11},...,a_{m1},...,a_{1n},...,a_{mn}]^{\top}\]

---